CLASS-10
EQUAL MATRICES
Equal Matrices –
Two matrices A & B are said to be equal, written as A = B, if and only if when –
(i) A and B are of the same order, i.e, they have the same number of rows and the same number of columns.
(ii) Their corresponding elements are equal.
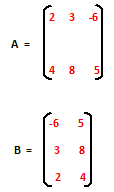
Example.1)

Above A and B matrices are equal, because both are of the same order (3 X 3) and their corresponding elements are equal. Hence we can write that A = B
Example.2) The matrices –
Above two matrices A & B are not equal, because A is a matrix or order (2 X 3) while B is a matrix of order (3 X 2)
Example.3) The matrices –

Above two matrices A & B are not equal, because (1, 1)th element of A ≠ (1, 1)th element of B, (1, 2)th element of A ≠ (1, 2)th elements of B, and (2, 3)th element of A ≠ (2, 3)th element of B, even though both matrices A and B are of the same order (2 X 3).
Hence, we can conclude that the matrices [x y] and [0 -4] are equal if and only if x = 0 and y = - 4.
Your second block of text...