CLASS-10
MULTIPLICATION OF MATRICES

Multiplication of Matrices –

(i) For any two matrices A & B, the product AB exists only, when –

Number of columns in A = Number of rows in B

(ii)  If A is an (m X n) matrix and B is an (n X p) matrix, then AB is an (m X p) matrix

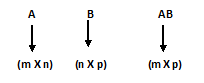
(iii)  (i, k)th element of AB = (i-th row of A) X (k-th column of B)

Product of two Matrices each of Order (2 X 2)

If A and B are matrices each of order (2 X 2), then AB is a (2 X 2) matrix given by –

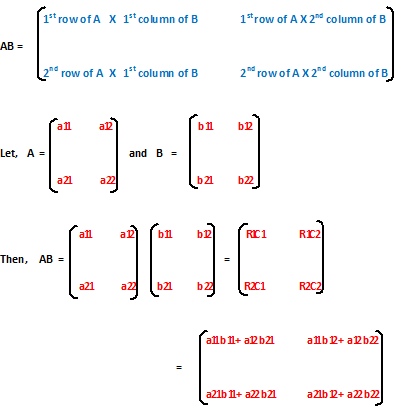
There are some examples are given below for your better understanding -

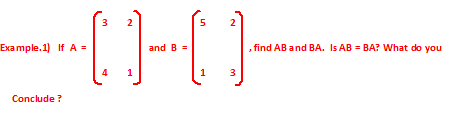
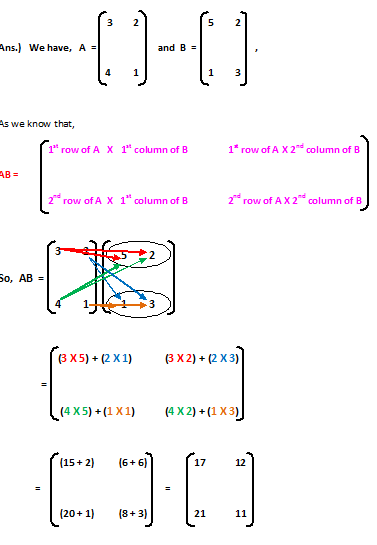
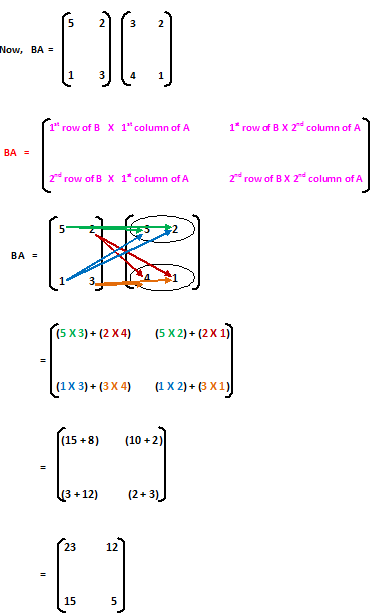
Clearly,  AB ≠ BA         (Ans.)

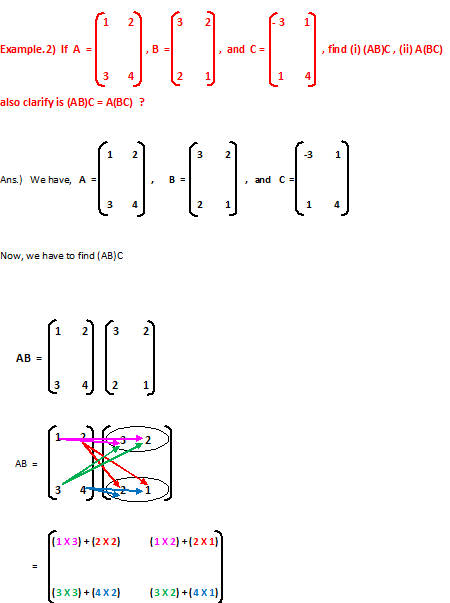
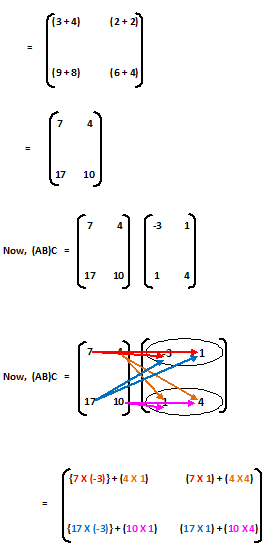
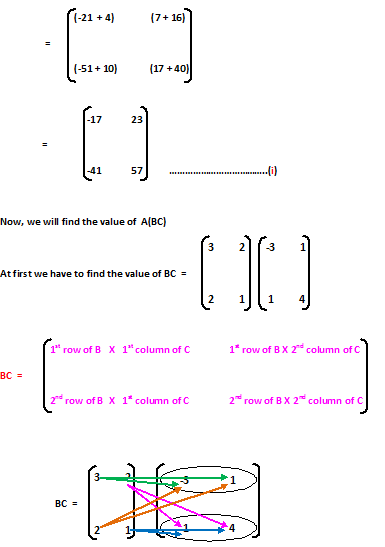
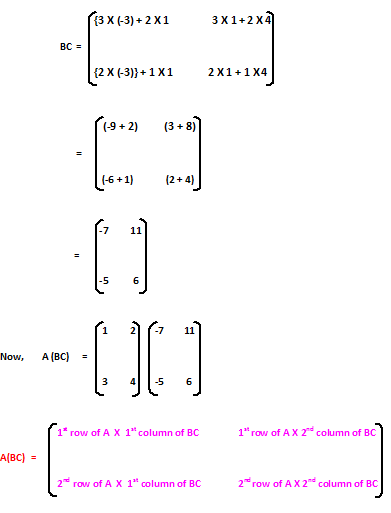
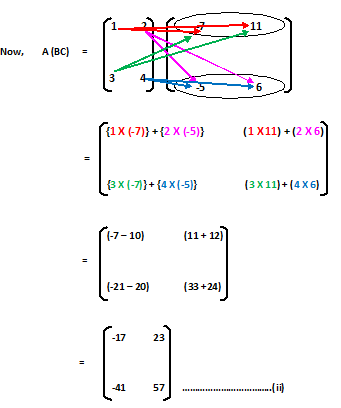
Clearly shown that,  (AB)C ≠ A(BC)                       (Ans.)

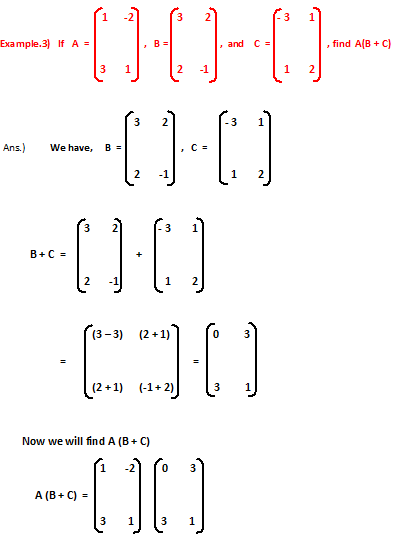
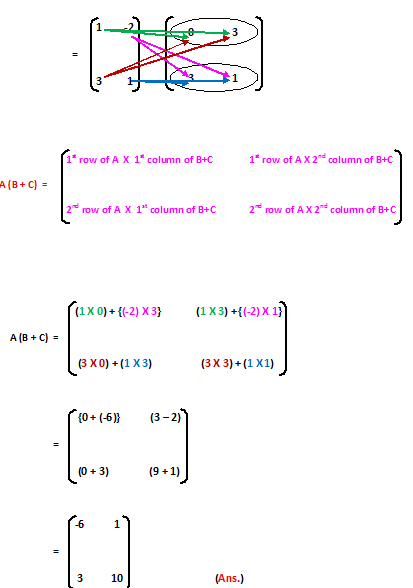
Your second block of text...