CLASS-10
MATRIX - PROBLEM & SOLUTION

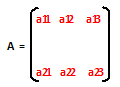
now, a₁₁ = (1 + 1) = 2, 

      a₁₂ = (1 + 2) = 3, 

     a₁₃ = (1 + 3) = 4,

      a₂₁ = (2 + 1) = 3,

      a₂₂ = (2 + 2) = 4,

      a₂₃ = (2 + 3) = 5,

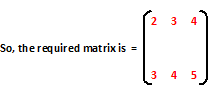
Example.2) If a matrix has 8 elements, what are the possible orders it can have ?

Ans.)  Since all matrices of order (1 X 8), (8 X 1), (2 X 4), or (4 X 2) contains 8 elements, a matrix containing 8 elements can have any of the following orders –

(1 X 8), (8 X 1), (2 X 4), or (4 X 2)         (Ans.)

Example.3) If a matrix has 12 elements, what are the possible orders it can have ?

Ans.)  Since all matrices of order (1 X 12), (12 X 1), (3 X 4), (4 X 3), (6 X 2), or (2 X 6) contains 12 elements, a matrix containing 12 elements can have any of the following orders –

(1 X 12), (12 X 1), (3 X 4), (4 X 3), (6 X 2), or (2 X 6)    (Ans.)

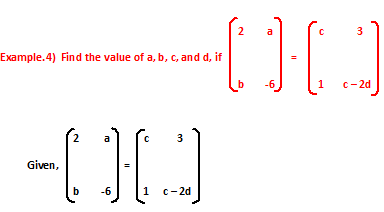
we know that the corresponding elements of equal matrices are equal.

So, 2 = c, a = 3, b = 1, and -6 = c – 2d

Thus we have, a = 3, b = 1, and  c = 2.

Also, -6 = c – 2d

=>   - 6 = 2 – 2d    (substitute the value of c = 2)

=>   - 2d = - 8

=>      d = 4

So, the value of a, b, c, & d is 3, 1, 2, & 4 respectively.   (Ans.)

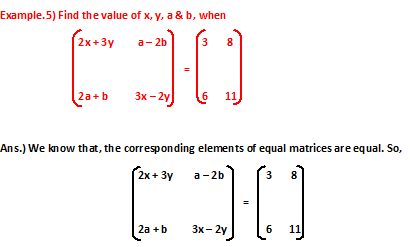
            2x + 3y = 3 ……………..(i)

         3x – 2y = 11 ……………….(ii)

          a – 2b = 8 ………………(iii)

          2a + b = 6 ………………(iv)

Multiplying (i) by 2 and multiplying (ii) by 3 and we get –

                 4x + 6y = 6 ……………(v)

                 9x – 6y = 33 …………..(vi)

Now, adding (v) and (vi), and we get –

                     4x + 6y = 6

                     9x - 6y =  33

                  -------------------

                         13x  = 39

              =>          x  =  3

Now putting the value of x = 3 in (v) and we get -

                          4x + 6y = 6

                   =>   (4 X 3) + 6y = 6

                  =>    12 + 6y = 6

                  =>    2 + y = 1

                  =>    y = - 2 + 1 = - 1

Multiplying (iii) by 1 and multiplying (iv) by 2 and we get –

                               a – 2b = 8 ………………(vii)

                             4a + 2b = 12 ………………(viii)

Now, we will add (vii) & (viii), and we get –

                               a – 2b = 8

                             4a + 2b = 12

                         -----------------

                                5a  =  20

                          =>       a = 4

Now, we will substitute the value of a = 4 in (iv), and we get -

                            2a + b = 6

                  =>      (2 X 4) + b  = 6

                  =>      8 + b = 6

                  =>      b = - 8 + 6 = - 2

Hence, a = 4, b = - 2, x = 3, and y = - 1           (Ans.)