CLASS-10
RATION & PROPORTION - PROBLEM & SOLUTION ON RATIO

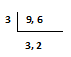
So, the product of common factor is = 3 X 3 X 2 = 18. So, the LCM of 9 & 6 is 18.

Now, we will find the factor of 18 by 9, i.e. 18 ÷ 9 = 2, so 9 X 2 = 18

And, we will find the factor of 18 by 6, i.e. 18 ÷ 6 = 3, so 6 X 3 = 18

Where, A : B = 4 : 9,

             4

L.H.S = -------

             9

Multiply numerator & denominator of said fraction by 2, and we get

     4 X 2          8

= --------- = ------

     9 X 2         18

Also we have, B : C = 6 : 5,

             6

R.H.S = ------

             5

Multiply numerator & denominator of said fraction by 3, and we get

    6 X 3         18

= -------- = -------

    5 X 3         15

As per the rules, L.H.S = R.H.S

   A          B

------ = ------

   B          C

Or, A : B : C

   8          18

------ = -------

  18          15

Hence, A : B : C = 8 : 18 : 15       (Ans.)

Example.4) If, 2 A = 3 B = 4 C, find A : B : C

Ans.) Let, 2 A = 3 B = 4 C = k (say)

               k             k              k

Then, A = ------, B = ------, C = ------

               2             3              4

                     k          k         k

So, A : B : C = ------ : ------ : ------

                     2          3         4

                    1        1        1

               = ----- : ----- : -----

                    2        3        4

                     1                 1                  1

               = (------ X 12) : (------ X 12) : (------ X 12) 

                     2                 3                  4

                               [Where, L.C.M of 2, 3, 4 is 12]

               =    6 : 4 : 3                (Ans.)

                   A          B         C

Example.5) If ------ : ------ : ------ Then find A : B : C

                   4          5         6

        A          B         C

Let, ------ : ------ : ------ = k.

        4          5          6

  So,  A = 4 k, B = 5 k, C = 6 k

Then,  A : B : C = 4 k : 5 k : 6 k

Hence,  A : B : C = 4 : 5 : 6         (Ans.)

Example.6) If, 2 A = 3 B, and 4 B = 5 C, then find -

(i) A : C, and (ii) A : B : C

Ans.) we have, 2 A = 3 B

      A         3

=> ----- = ------

      B         2

=>    4 B = 5 C

       B          5

=> ------ = -------

       C          4

       A           A           B

(i) ------- = ------- X -------

       C           B           C

     3           5           15

= ------ X ------- = -------

     2           4            8

=> A : C = 15 : 8                (Ans.)

                 A           3          B           5

(ii) we have ------- = -------, ------- = -------

                 B           2          C           4

As we can notice that, there are two different values of B obtained from two different fraction. L.C.M of 2 & 5 is 10.

Now, we will find the factor of 10 by 2, i.e. 10 ÷ 2 = 5, so 2 X 5 = 10

And, we will find the factor of 10 by 5, i.e. 10 ÷ 5 = 2, so 5 X 2 = 10

Where, A : B = 3 : 2,

             3

L.H.S = ------

             2

Multiply numerator & denominator of said fraction by 2, and we get

     3 X 5         15

= --------- = ------

     2 X 5         10

Also we have, B : C = 5 : 4,

             5

R.H.S = ------

             4

Multiply numerator & denominator of said fraction by 3, and we get

     5 X 2         10

= --------- = ------

     4 X 2          8

As per the rules, L.H.S = R.H.S

    A           B

------- = --------

    B           C

Or,  A : B : C

   15          10

------- = -------

   10           8

Hence, A : B : C = 15 : 10 : 8         (Ans.)

Example.7) If (4a + 3b) : (6a + 5b) = 11 : 17, find a : b

Ans.) Given, (4a + 3b) : (6a + 5b) = 11 : 17

      (4a + 3b)         11

=> ----------- = --------

      (6a + 5b)         17

=> 17 (4a + 3b) = 11 (6a + 5b)

=> 68a + 51b = 66a + 55b

=> 68a – 66a = 55b – 51b

=> 2a = 4b

=> a = 2b

       a          2

=> ------ = ------

       b          1

=>  a : b = 2 : 1          (Ans.)     

Example.8) If (4x²+ xy) : (3xy - y²) = 12 : 5, find x : y

Ans.) Given, (4x²+ xy) : (3xy - y²) = 12 : 5

      (4x²+ xy)        12

=> ----------- = -------

      (3xy - y²)        5

           x²          xy

     4 (------) + (------)               12

           y²          y²

=> ------------------------- = --------- 

           xy         y²

      3 (-----) - -----                   5

           y²         y²

                  [On dividing numerator & denominator by y²]

             x             x

       4 (------)² + (------)              12

             y             y

=> --------------------------- = ---------

                 x

           3 (------) - 1                     5

                 y

         x

Let, ------ = a , and we get -

         y

       4a² + a          12

=> ----------- = --------

       3a – 1            5

=> 5 (4a²+ a) = 12 (3a – 1)

=> 20a²+ 5a = 36a – 12

=> 20a²+ 5a - 36a + 12 = 0

=> 20a²- 31a + 12 = 0

=> 20a²- (15 + 16) a + 12 = 0

=> 20a²- 15a – 16a + 12 = 0

=> 5a (4a – 3) – 4 (4a – 3) = 0

=> (4a – 3) (5a – 4) = 0

=> (4a – 3) = 0 or (5a – 4) = 0

=> a = 3/4 or a = 4/5

                                               x

Now we will substitute the value of a = ------- , and we get -

                                               Y

       x          3            x           4

=> ------ = ------, or ------- = ------

       y          4            y           5

=> x : y = 3 : 4  or  x : y = 4 : 5     (Ans.)

Example.9) A ratio is equal to 5 : 7. If its antecedent is 35, what is the consequent ?

Ans.) Let the consequent be ‘x’. then –

Antecedent : Consequent

=> 5 : 7 = 35 : x

       5         35

=> ------ = ------

       7          x

=>  5x = (35 X 7)

=>   x = 49

Hence the consequent is 49       (Ans.)

Example.10) The ratio between two numbers is 5 : 6 and their LCM is 150. Find the numbers.

Ans.) Let the required numbers be 5x & 6x

Then, LCM of 5x and 6x is 30x

Now, 30x = 150

=> x = 150/30 = 5

So, one number = (5 X 5) = 25, other number = (6 X 5) = 30

Hence the required numbers are 25 & 30       (Ans.)