CLASS-10
MEAN - PROBLEM & SOLUTION

Ans.)  From the given data, we may prepare the table given below –

Class Interval    Class Mark (xₐ)   Frequency (fₐ)      (fₐ X xₐ)

  80 – 100              90                 20                1800

 100 – 120            110                 30                3300

 120 – 140            130                 20                2600

 140 – 160            150                 40                6000

 160 – 180            170                 90               15300

                                       ∑fₐ = 200          ∑fₐxₐ = 29000

                       ∑fₐxₐ         29000

   Mean =  --------- = --------- = 145

                 ∑fₐ            200

so, the required mean value is 145.     (Ans.)

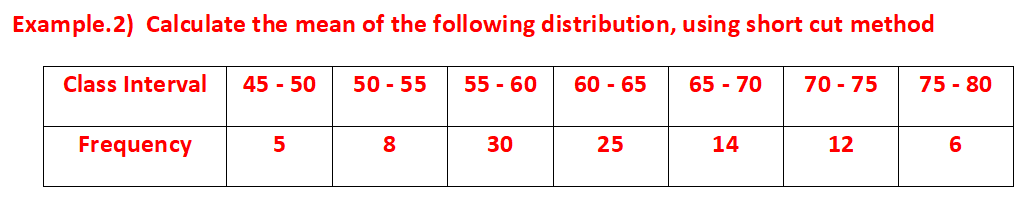
Ans.)  From the given data, we may prepare the frequency distribution table as under –

                                           60 + 65        125

Let, the assumed mean would be, A = --------- = -------- = 62.5

                                               2             2

Class Interval   Mid Value(xₐ)   Frequency(fₐ)  dₐ = (xₐ - A)   fₐ X dₐ

    45 – 50          47.5               5             -15           -75

    50 – 55          52.5               8             -10           -80

    55 – 60          57.5              30              -5          -150

    60 – 65        62.5 = A           25               0              0

    65 – 70          67.5              14               5             70

    70 – 75          72.5              12              10            120

    75 – 80          77.5               6              15             90  

                                     ∑fₐ = 100                  ∑fₐdₐ = -25

                                            ∑fₐdₐ

Hence the mean is given by x =  A + ---------

                                             ∑fₐ

                                              (-25)

                                =  62.5 + -------- = 62.5 – 0.25

                                              100

                                =  62.25

Hence the mean of the given data is 62.25      (Ans.)

Ans.) The given class intervals are in inclusive form. So, we convert them into exclusive form, and prepare the table as given below –

Marks Class    Mark (xₐ)   No of Students (fₐ)    dₐ = xₐ-A     fₐ X dₐ

                                                     = xₐ- 45.5 

10.5 – 20.5     15.5              2                -30            -60

20.5 – 30.5     25.5              6                -20           -120

30.5 – 40.5     35.5             10               -10            -100

40.5 – 50.5     45.5 = A        12                  0               0

50.5 – 60.5     55.5              9                 10              90

60.5 – 70.5     65.5              7                 20             140

70.5 – 80.5     75.5              4                 30             120  

                                ∑fₐ = 50                         ∑fₐdₐ = 70

                            ∑fₐdₐ                   70

No, the Mean =  A  + --------- = (45.5 + ------)

                             ∑fₐ                    50

                                      =  (45.5 + 1.4)

                                      =  46.9

So, the required mean value is 46.9.  (Ans.)

Example.4)  If the mean of 7, 10, 4, 12, x, 3 is 7.5, find ‘x’

Ans.)  Sum of the given numbers = (7 + 10 + 4 + 12 + x + 3)

                                     = (36 + x)

Total number of given numbers = 7                                                                                                           

As per the given condition, mean of the given numbers

                            (36 + x)

                       = ---------- =  7.5   

                               6

                                                                                     Or,  (36 + x) = 45

                                                                                     Or, x = (45 – 36)  =  9

So, the required number is 9    (Ans.)

Example.5) The marks obtained by 15 students in a class test are =>  15, 10, 14, 11, 17, 7, 14, 15, 9, 12, 9, 6, 11, 8, 16.

Find  (i)  Their mean marks

      (ii) The mean of their marks, when the marks of each student are increased by 2

      (iii) The mean of their marks, when 3 marks are deducted from the marks of each students.

      (iv) The mean of their marks, when the marks of each student are tripled.

Ans.) Sum of all the marks = (15 + 10 + 14 + 11 + 17 + 7 + 14 + 15 + 9 + 12 + 9 + 6 + 11 + 8 + 16) = 174

Number of students = 15

                    174

Mean number = ------- = 11.6   ………………………….(i)     (Ans.)

                    15

On increasing 2 marks of each students, total mark is increased = (15 X 2) = 30 marks

New sum of all the marks = 174 + 30 = 204

Number of students = 15

                       304

Mean marks now = ------- = 20.26 …………………………(ii)       (Ans.)

                        15

On decreasing 3 marks of each, marks decreased = (15 X 3) = 45

Now, new sum of all the marks = (174 – 45) = 129

Number of students = 15

                        129

Mean marks now = --------  =  8.6  …………………….(iii)     (Ans.)

                        15

On tripling the marks of each, the sum is tripled.

New sum of all the marks = (174 X 3) = 522

Number of students = 15

                        522

Mean marks now = --------  = 34.8  ………………………..(iv)        (Ans.)

                        15