CLASS-10
MEDIAN-QUARTILES-MODE- PROBLEM & SOLUTION

Find the median diameter in mm.

Ans.) Arranging the given terms in an ascending order and preparing the cumulative frequency table, we have –

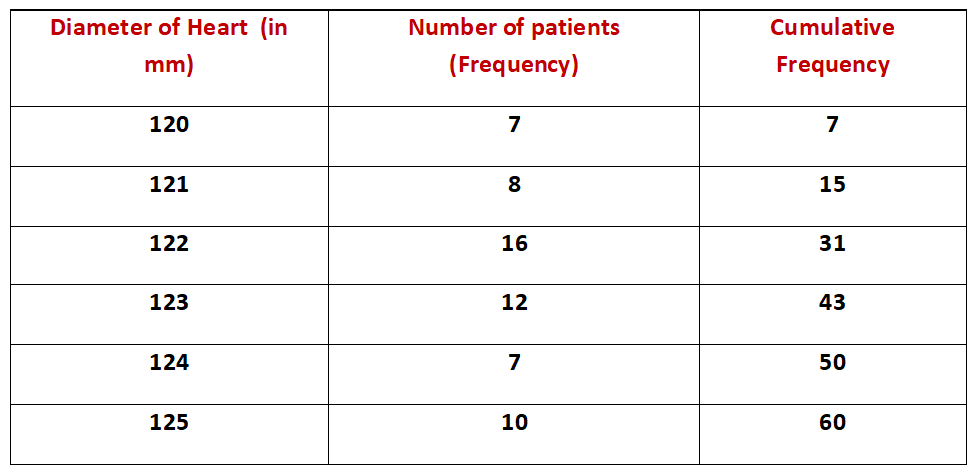
So,  n  =  60,

       n

=> ------ =  30

       2

           n

And,  ------- +  1  = 30 + 1 =  31

           2

Clearly  n is even number

                  1          n                          n

So, median = ------ { (-----)th observation + (------ + 1)th 

                  2          2                          2

observation}

                    1

               = ----- (30th observation + 31st observation)

                    2

But, from the above table, we find that each patient from 16th to 31st has an heart of diameter 122 mm

                              1

So, Median Diameter =  ------ (22 + 22) mm

                              2

                             1

                       = ------- X  44 mm  =  22 mm       (Ans.)

                             2

Example.3) The height (in cm) of 50 students of a class are given below –

Find – (i) Median                (ii) First Quartile

       (ii) Third Quartile       (iv)  Interquartile Range

Ans.)   Arranging the given heights in an ascending order, we may prepare the cumulative frequency table as shown below –

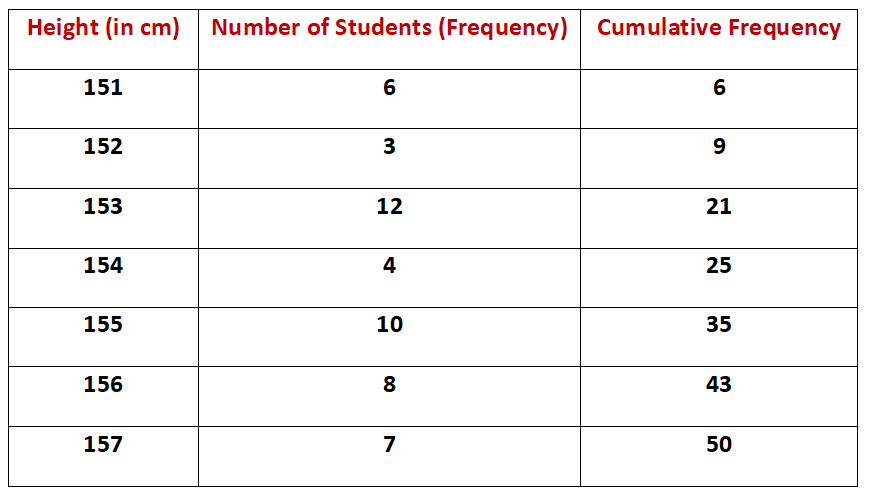
Where, n = 50, which is even.

                1        n                          n

(i) Median = ----- {(-----)th observation + (----- + 1)th observation}

                2        2                          2

             1        50                         50

        = ----- {(------)th observation + (------ + 1)th observation}

             2        2                           2

             1                                                   

        = ------ {25th observation + 26th observation}

             2        

              (154 + 155)        309

         = ------------- = -------- =  154.5     (Ans.)

                   2                2

                               n

(ii) First quartile, Q₁ =  (------)th observation

                               4

                              50

                       =  (------)th observation = 12.5th observation

                              4                      

                       =  13th observation

But, each student from 10th 21st has a height of 153cm.  

Hence, Q₁ = 153       (Ans.)

                               3n

(iii) Third quartile, Q₃ = (------)th observation

                               4

                              3 X 50

                         = (---------)th observation

                                 4

                         = 37.5th observation = 38th observation

But, each student from 36th to 43rd has a height of 156 cm

Hence, Q₃ = 156      (Ans.)

(iv) Interquartile Range = (Q₃ - Q₁)  = (156 – 153) cm  =  3 cm  (Ans.)

Example.4)  The distribution given below shows the marks obtained by 25 students in aptitude test. Find the mean, median, and mode of the distribution –

Ans.)  We may prepare the cumulative frequency as under-

Marks Obtained(a)   Number of Students(f)   Cumulative Frequency   f X a

       5                       3                        3                1

       6                       9                       12               54

       7                       6                       18               42

       8                       4                       22               32

       9                       2                       24               18

      10                       1                       25               10

                            ∑f = 25 (n)                            ∑fa= 171

            ∑fa          171

Mean = -------- = -------- = 6084

            ∑f            25

Here, n = 25, which is odd

                       25 + 1

Median = value of (---------)th term = value of 13th term = 7

                          2

Since, the frequency of 6 is maximum, so mode = 6

Hence Mean = 6.84, Median = 7, and Mode = 6          (Ans.)