CLASS-10
TRIGONOMETRY - HEIGHT AND DISTANCE - PROBLEM & SOLUTION
There are some important problem & solution has given below to clear concept about Trigonometry - Height & Solution
Example.1) A vertical pole and a vertical tower are on the same level ground. From the top of the pole, the angle of elevation of the top of the tower is 60⁰ and the angle of depression of the foot of the tower is 30⁰. Find the height of the tower if the height of the pole is 20 m
Ans.) Let, AB be the pole and CD be the tower.
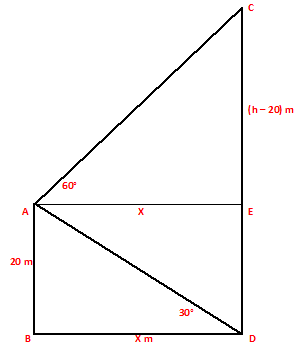
Draw AE ⊥ CD. Then,
AB = 20 m, ∠CAE = 60⁰ and ∠ADB = 30⁰
Let, BD = x m and CD = h meters
Then, CE = (CD – ED) = (CD – AB) = (h – 20) m
From right △ABD, we have
AB
------- = tan 30⁰
BD
20 1
=> ------- = -------
x √3
=> x = 20 √3 …………………..……….(i)
Clearly, AE = BD = x meters
From right △AEC, we have
CE
-------- = tan 60⁰
AE
(h – 20)
=> ---------- = √3
x
(h – 20)
=> x = ------------ …………………………(ii)
√3
Equating the value of x from (i) and (ii), we get –
(h – 20)
20 √3 = -----------
√3
=> (h – 20) = (20√3 X √3)
=> h = (20 + 60) = 80
Hence the height of the tower is 80 m (Ans.)
Example.2) In the figure given, from the top of a building AB = 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30⁰ and 60⁰ respectively. Find –
(i) The horizontal distance between AB & CD
(ii) The height of the lamp.
Ans.) Let, AX be the horizontal line
Draw DE ǁ CB. Then,
∠ADE = 30⁰ and ∠ACB = 60⁰
Let, CB = DE = x meters
And CD = BE = y meters
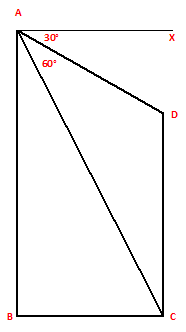
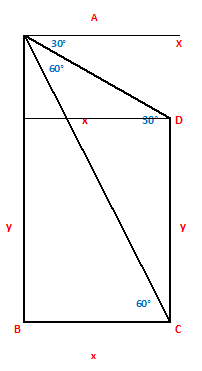
Then, AE = (60 – y) m
From right △ABC, we have –
AB
-------- = tan 60⁰
BC
60
=> -------- = √3
x
=> x = 20 √3 …………………(i)
From right △AED, we have –
AE
-------- = tan 30⁰
ED
(60 – y) 1
=> ---------- = ------
x √3
=> x = (60 – y) √3 …………………………..(ii)
Equating the value of x from (i) and (ii), we get –
20√3 = (60 – y) √3
=> 20√3 = 60√3 - √3y
=> √3y = 60√3 - 20√3
=> √3y = 40√3
=> y = 40
Thus the horizontal distance between AB & CD is 20√3 = 34.64 m …………..(i) (Ans.)
And, the height of the lamp post is 40 m ……………………(ii) (Ans.)
Example.3) As observed from the top of a 80 m tall light house, the angles of depression of the two ships on the same side of the light house in horizontal line with its base are 30⁰ and 40⁰ respectively. Find the distance between the two ships. Give your answer correct to the nearest meters.
Ans.) Let AB be the lighthouse and C and D be the two ships
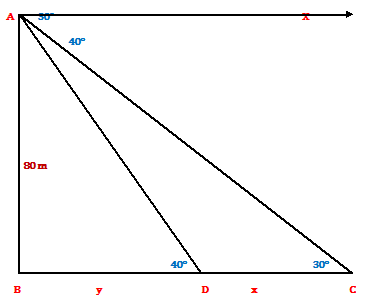
Let, AX be the horizontal line. Then,
AB = 80 m, ∠ACB = ∠CAX = 30⁰ and ∠ADB = ∠DAX = 40⁰
Let, CD = x meters and DB = y m
From right △ABD, we have
AB
-------- = tan 40⁰
DB
80
=> ------- = 0.84
y
80
=> y = -------- = 95.24
0.84
From right △ABC, we have –
AB
------- = tan 30⁰
CB
80 1
=> -------- = ------
x + y √3
=> (x + y) = 80 √3 = (80 X 1.732) [where, √3 = 1.732]
= 138.56
Now, CD = x = (x + y) – y = (138.56 – 95.24)
= 43.32
Hence, the required distance between the two ships is 43 m. (Ans.)
Example.4) The shadow of a tower, when the angle of elevation of the sun is 45⁰, is found to be 10 m longer than when it was 60⁰. Find the height of the tower.
Ans.) Let AB be the tower and let AC and AD be the shadows of the tower at the two instants. Then,
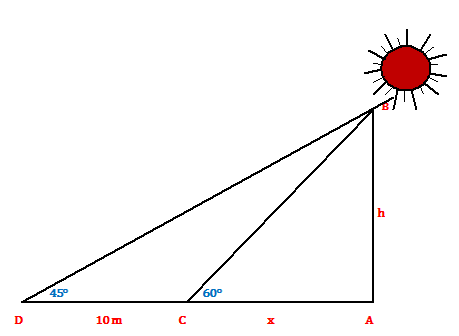
∠ACB = 60⁰, ∠ADB = 45⁰, and CD = 10 m.
Let, CA = x meters and AB = h meters
From right △DAB, we have
AD
------- = cot 45⁰
AB
10 + x
=> --------- = 1,
h
=> h = (10 + x)
=> x = (h – 10) ……………………………(i)
Again from right △CAB, we have –
AC
----------- = cot 60⁰
AB
x 1
=> ------- = -------
h √3
h
=> x = ------- …………………….(ii)
√3
Equating the value of x from (i) and (ii), we get –
h
(h – 10) = -------
√3
=> (h – 10)√3 = h
=> √3 h - 10√3 = h
=> √3h – h = 10√3
=> (√3 – 1)h = 10√3
10√3
=> h = -----------
(√3 – 1)
10√3 (√3 + 1)
=> h = --------- X ------------
(√3 – 1) (√3 + 1)
10√3 (√3 + 1) 10√3 (√3 + 1)
=> h = ----------------- = ----------------
(3 – 1) 2
=> h = 5√3 (√3 + 1)
=> h = {5 X (√3)²} + 5√3
=> h = 15 + (5 X 1.732) = (15 + 8.66)
=> h = 23.66
Hence the height of the tower is 23.66 m. (Ans.)
Your second block of text...