CLASS-10
TRIGONOMETRY- CORE CONCEPTS OF HEIGHT & DISTANCE

HEIGHT & DISTANCE –


This chapter deals with very practical chapter of Trigonometry in determining such parameters as height of objects like a mountain, a tree, a tower, tall building, a tall post, or a pillar, etc., and breadth of a river, etc., which are otherwise very difficult to measure.

Some Important Definition –

Line of Sight – When the eye of a person at a point O looks at an object A, then the line OA is called the line of sight.

(i) Angle of Elevation –

Suppose a man from a point O, looks up at an object A, placed above the level of his eye. Then, the angle which the line of sight makes with the horizontal through O, is called the Angle of Elevation of A as seen from O.         

Class-10-Height-and-Distance-1.png

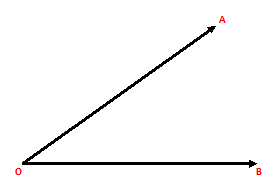
Let, OB be a horizontal line. Let a man at O on the level ground be looking up towards an object P, say an aeroplane or the top of a tower or the flag at the top of a building.

Then, ∠BOA is the angle of elevation of P as seen from O.

(ii) Angle of Depression –

Suppose a man from a point O, looks down at an object A, placed below the level of his eye. Then, the angle which the line of sight makes with the horizontal through O, is called the angle of depression of A as seen from O.

Class-10-Height-and-Distance-2.png

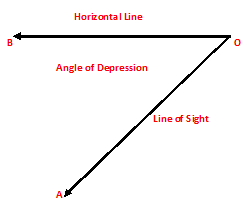
Let, BO be a horizontal line. Let a man at O, on the top of a tower be looking down towards an object A, say a ship in the sea.

Class-10-Height-and-Distance-3.png

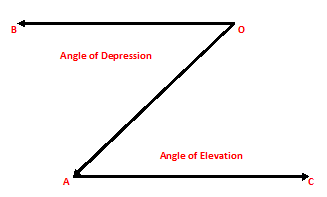
Then, ∠BOA is the angle of depression of A as seen from O.

An Important Information – Angle of depression of A as seen from O = Angle of elevation of O as seen from A.

So, ∠BOA = ∠CAO

There are some examples are given below for your better understanding -

Example.1) The angle of elevation of the top of a tower at a distance of 90 meters from its foot on a horizontal plane id found to be 30⁰. Find the height of the tower

Ans.)  Let AB be the tower and O be the point of the observation. Then OA = 90 m, and ∠OAB = 90⁰, and ∠AOB = 30⁰

Class-10-Height-and-Distance-4.png

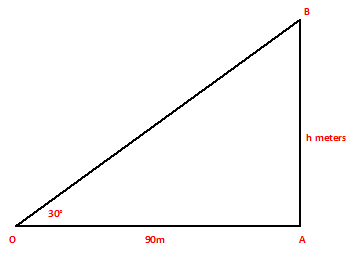
                                                                   AB

Let, AB = h meters, Then from right △OAB, we have ------ = tan 30⁰

                                                             OA

             h             1

    =>  -------- = --------

            90            √3

                                                                                                   90

    =>    h  =  -------- =  30√3

                     √3

                                                                          =>    h  = (30 X 1.732) m      [√3 = 1.732]

                                                                          =>    h  =  51.96 m       

Hence, the height of the tower is 51.96 m     (Ans.)



Example.2) A kite is flying at a height of 75 m from the level ground, attached to a string inclined at 60⁰ to the horizontal. Find the length of the string to the nearest meter.

Ans.)  Let OX be the horizontal line and A be the position of the kite with string OA

Draw AB ⊥ OX

Class-10-Height-and-Distance-5.png

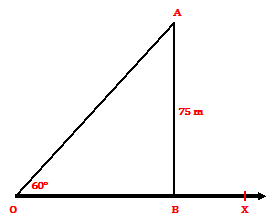
Then, AB = 75 m and ∠BOA = 60⁰

From right △OBA, we get

           AB

       -------- =  sin 60⁰

           OA


         75           √3

=>   -------- = -------

         OA           2


         OA           2

=>   -------- = -------

         75           √3


                  75 X 2          50 X 3

=>   OA  =  ----------- = ----------

                    √3               √3


=>     OA = (50 X √3)  =  (50 X 1.732)         [where, √3 = 1.732]

                                         =  86.6 m 

Hence, the length of the string to the nearest meter is 87 m.    (Ans.)

Your second block of text...