CLASS-10
TRIGONOMETRY - SQUARE RELATIONS
Square Relations –
Theorem 3. For an acute angle, prove that :
(i) sin² A + cos² A = 1,
(ii) 1 + tan² A = sec² A,
(iii) 1 + cot² A = cosec² A
proof : We have,
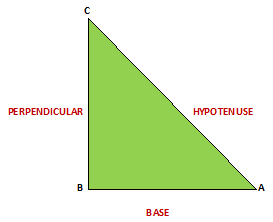
BC AB
(i) sin² A + cos² A = (-------)² + (-------)²
AC AC
BC² AB²
= -------- + --------
AC² AC²
AB² + BC²
= ---------------
AC²
AC²
= ------- = 1 [AB² + BC² = AC²]
AC²
Hence, sin² A + cos² A = 1 (Proved)
BC BC²
(ii) 1 + tan² A = 1 + (------)² = 1 + ------
AB AB²
AB² + BC²
= -------------
AB²
AC²
= --------
AB²
AC
= (-------)² = sec² A
AB
Hence, 1 + tan² A = sec² A (Proved)
AB AB²
(iii) 1 + cot² A = 1 + (------)² = 1 + -------
BC BC²
BC² + AB²
= ------------
BC²
AC²
= --------
BC²
AC
= (-------)² = cosec² A
BC
Hence, 1 + cot² A = cosec² A (Proved)
There are some examples are given below, for your better understanding -
sin A (1 + cos A)
Example.1) Prove that, ------------ + -------------- = 2 cosec A
(1 + cos A) sin A
sin A (1 + cos A)
Ans.) We have, L.H.S = -------------- + ----------------
(1 + cos A) sin A
sin² A + (1 + cos A)²
= ------------------------
sin A (1 + cos A)
sin² A + 1 + 2 cos A + cos² A
= --------------------------------
sin A (1 + cos A)
(sin² A + cos² A) + 1 + 2 cos A
= ----------------------------------
sin A (1 + cos A)
[where, sin² A + cos² A = 1]
1 + 1 + 2 cos A
= --------------------
sin A (1 + cos A)
2 + 2 cos A
= -------------------
sin A (1 + cos A)
2 (1 + cos A)
= ------------------
sin A (1 + cos A)
2
= ---------
sin A
= 2 cosec A = R.H.S [1/ sin A = cosec A]
Hence, L.H.S = R.H.S (Proven)
Example.2) Prove that, (cosec A – sin A) (sec A – cos A) sec² A = tan A
Ans.) We have, L.H.S = (cosec A – sin A) (sec A – cos A) sec² A
1 1
= (-------- - sin A) (-------- - cos A) sec² A
sin A cos A
1 - sin² A 1 - cos² A
= (-------------) (-------------) sec² A
sin A cos A
cos² A sin² A
= (-------------) (------------) sec² A
sin A cos A
[where, 1 - sin² A = cos² A, and 1 - cos² A = sin² A]
sin A . cos A
= -----------------
cos² A
sin A
= ----------
cos A
= tan A [where, sin A/cos A = tan A]
L.H.S = R.H.S (Proven)
Your second block of text...