CLASS-10
VOLUME & SURFACE AREA OF THE SOLID - CONE
CONE –
Right Circular Cone – If a right angled triangle is revolved about one of the sides containing the right angle, then the solid thus generated, is called a right circular cone. Thus, when a right angled triangular lamina AOB is revolved about OA, it generates a cone.
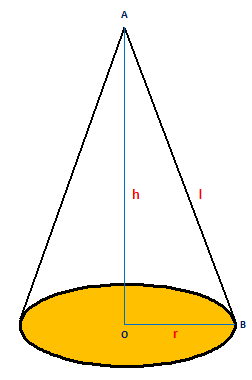
The point A is called the vertex of the cone.
The length OA = h, is called the height of the cone.
The base of a cone is a circular with O as center and OB as radius.
The length OB is called the radius of its base = r
The length AB is called the slant-height of the cone = l
In the right angled AOB, we have
l² = h² + r² and therefore, l = √(h² + r²)
Formulae –
For a right circular cone of Radius = r, Height = h, & Slant Height = l,
We have
1
(i) Volume of the cone = (------ πr²h) cubic units
3
(ii) Area of the curved surface or Lateral surface of the cone
= (πrl) sq units = [πr√(h² + r²)] sq. Units
(iii) Total surface area of the cone = (Curved Surface Area + Area of Base)
= (πrl + πr²) sq. units
= πr (l + r) sq. Units
There are some examples are given below for your better understanding -
Example.1) The height of a cone is 20cm and the radius of its base is 15 cm.
Find – (i) The slant height of the cone,
(ii) The lateral surface area of the cone,
(iii) The total surface area of the cone,
(iv) The volume of the cone.
Ans.) Here, h = 20 cm, and r = 15 cm.
(i) Slant height, l = √(h² + r²)
= √(20² + 15²) cm
= √625 cm = 25 cm (Ans.)
(ii) The total surface area of the cone = πrl
= (3.14 X 15 X 25) cm²
= 1177.5 cm² (Ans.)
(iii) Total surface area = πr(l + r)
= [3.14 X 15 (25 + 15)] cm²
= 1884 cm² (Ans.)
1 1
(iv) Volume = ------ πr²h = [------ X 3.14 X 15² X 20] cm³
3 3
= 4710 cm³ (Ans.)
Example.2) The volume of a conical tent 1232 m³and the area of a base floor is 154 m²
Calculate – (i) The radius of the floor
(ii) The height of the tent
(iii) The length of the canvas to cover this conical tent, it being given that the width of the canvas in 2 m
Ans.) Let, area of the of the tent = πr²
So, πr² = 154
22
=> ------- X r² = 154
7
=> r² = 7 X 7
=> r = 7 m ......................(i) (Ans.)
Now, as per the given condition -
1
Volume of the Tent = ------- πr²h
3
1 22
So, ------- X ------- X 7² X h = 1232
3 7
=> (22 X 7) h = 1232 X 3
(1232 X 3)
=> h = ------------ = 24 m ............(ii) (Ans.)
22 X 7
Now, the lateral length of the cone, l = √(h² + r²)
= √(24² + 7²)
= √(576 + 49) = √625 = 25 m
So, the Slant height of the tent is 25 m
So, area of canvas required = curved surface area of the tent = πrl
22
= ------ X 7 X 25 = (22 X 25) = 550 m²
7
As per the condition, width of the canvas = 2 m
Area
Length of the canvas = ----------
Width
550
= -------- = 275 m ................(iii) (Ans.)
2
Example.3) A circus tent is in the form of a cylinder surmounted by a cone. The height of the tent above the ground in 85 m and the height of the cylindrical part is 50 m. If the diameter of the base is 168 m, find the quantity of canvas required to make the tent. Allow 20% extra for folds and stitching. Give the answer to the nearest m².
168
Ans.) Radius of the tent, r = (------) m = 84 m
2
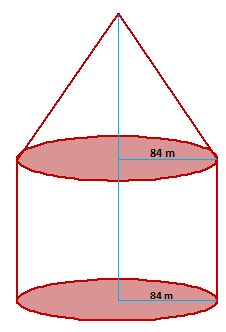
Height of the cylindrical part, H = 50 m.
Height of the conical part, h = (85 – 50) m = 35 m
Slant height of the conical part, l = √(h² + r²)
= √(35² + 84²) m
= √8281 m
= 91 m
Quantity of canvas required for the tent
= Curved Surface area of the tent
= Sum of the curved surface areas of cylindrical part and the conical part
= (2πrH + πrl) = πr (2H + l)
22
= [------ X 84 X {(2 X 50) + 91}] m²
7
= (22 X 12 X 191) m²
= 50424 m²
Area of canvas required for folds and stitching
= (20% of 50424) m²
20 50424
= (------ X 50424) m² = --------- m²
100 5
= 10084.80 m²
Total quantity of canvas required to make the tent
= (50424 + 10084.80) m²
= 60508.8 m² = 60509 m² (Ans.)
Your second block of text...