CLASS-11
RELATION & FUNCTION - FUNCTION AS A TYPE OF MAPPING

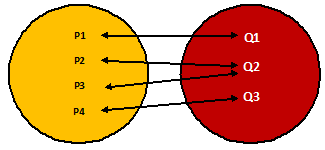
Function as a mapping

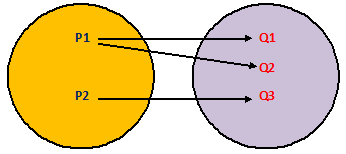
This mapping is not a function.

For the definition of a function to be satisfied, it is essential that each element of the domain is mapped into a unique element of the co-domain. If this condition is not met, the mapping is not a function. In terms of the pictures, for a mapping to be function, each arrow should emanate from a different point in the domain. Whether they terminate at the same point in the codomain is immaterial in the definition.

Remark – consider the following mapping. From the figure displaying the association of a player to the game he or she plays, we observe that the player C.Ronaldo of set A is not associated with any game in set B.

Remark – consider the following mapping. From the figure displaying the association of a player to the game he or she plays, we observe that the player C.Ronaldo of set A is not associated with any game in set B.

This association or mapping is not a function.

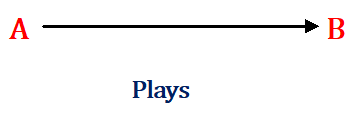
This association or mapping is not a function.

Essential Requirements For The Definition Of a Function –

A function f : A → B is defined under the following condition –

(i) Every x ∈ A is associated with some y in B, i.e., a function is defined only when the domain is entirely “used up”. The set B may not be entirely “used up” by the function.

(ii) The function may associate more than one ‘x’ to the same ‘y’.

(iii) No element in A should have more than one image in B.