CLASS-11
RELATION & FUNCTION-TYPES OF FUNCTION-INJECTIVE FUNCTION (ONE-ONE)
One-One Function (Injective Function) –
1.) A function f : A → B is called a one-one or injective function if distinct elements of A have distinct images in B, i.e., if a₁, a₂ ∈ A and a₁ ≠ a₂
=> f(a₁) ≠ f(a₂)
Equivalently, we say f : A → B is one-one if and only if for all a₁ a₂ ∈ A, f(a₁) = f(a₂)
=> a₁ = a₂
In terms of picture, we say that in one – one function, no more than one arrow terminates at any given element of B.
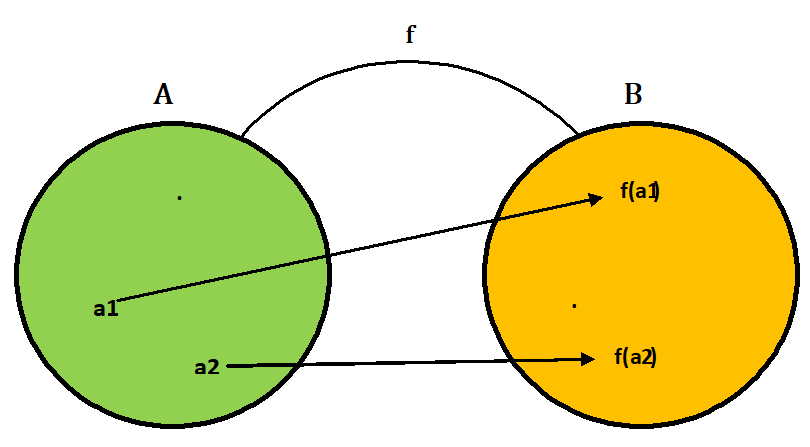
Illustration -
1) If A = {4, 5, 6} and B = {a, b, c, d} and if f : A → B such that f = {(4, a), (5, b), (6, c)}, then f is 1 – 1
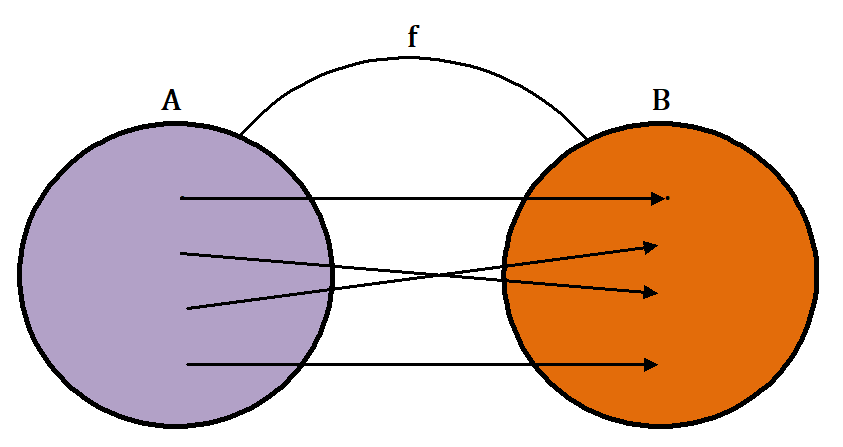
2) The mapping f : R → R such that f(x) = x² is not a one-one function since f(-2) = 4 and f(2) = 4, that is, two distinct elements – 2 and 2 have the same image 4.
Example.1) Find whether the following functions are one-one or not.
(i) f : R → R, defined by f(x) = x³, x ∈ R
(ii) f : Z → Z, defined by f(x) = x² + 5 for all x ∈ Z
5x + 7
(iii) f : R – {3} → R, defined by f(x) = ----------, x ∈ R – {3}
x – 3
Method of check whether a function is one-one or not –
Step.1) Take two arbitrary elements a₁, a₂ in the domain of f
Step.2) Put f(a₁) = f(a₂) and solve the equation
Step.3) If it yields a₁ = a₂, only then f : A → B is a one-one function otherwise not.
Remark. Let f : A → B and let a₁, a₂ ∈ A. Then a₁ = a₂ => f(a₁) = f(a₂) is always true from the definition, but f(a₁) = f(a₂) => a₁ = a₂ is true only when f is one-one.
Sol. (i) Let a₁, a₂ be two arbitrary elements of domain f, (a₁, a₂ ∈ R) such that f(a₁) = f(a₂)
Then f(a₁) = f(a₂) => a₁³ = a₂³ => a₁ = a₂
Hence, f is a one-one function.
(ii) Let a₁, a₂ be two arbitrary elements of Z such that f(a₁) = f(a₂) => a₁² + 5 = a₂² + 5
=> a₁² = a₂²
=> a₁ = ± a₂
Since f(a₁) = f(a₂) does not yield a unique answer a₁ = a₂ but gives a₁ = ± a₂, so f is not a one-one function.
In fact, we have f(2) = 2² + 5 = 9 and f(- 2) = (- 2)² + 5 = 9.
Thus two distinct elements 2 and – 2 have the same image.
5a₁ + 7
(iii) We have f(a₁) = ----------, x ∈ R – {3}
a₁ - 3
let, a₁, a₂ be two arbitrary elements of domain f(a₁, a₂) ∈ R – {3} such that f(a₁) = f(a₂)
5a₁ + 7 5a₂ + 7
Then, f(a₁) = f(a₂) => ----------- = -----------
a₁ - 3 a₂ - 3
=> 5a₁a₂ + 7a₂ - 15a₁ - 21 = 5a₁a₂ + 7a₁ - 15a₂ - 21
=> - 15 a₁ - 7 a₁ = - 15 a₂ - 7 a₂
=> - 22 a₁ = - 22 a₂
=> a₁ = a₂
So, f is one-one
Example.2) Show that the modulus function f : R → R, given by f(x) = ǀxǀ, is not one function
Ans.) given => f(x) = ǀxǀ
=> f(1) = ǀ1ǀ = 1 and f(- 1) = ǀ- 1ǀ = 1
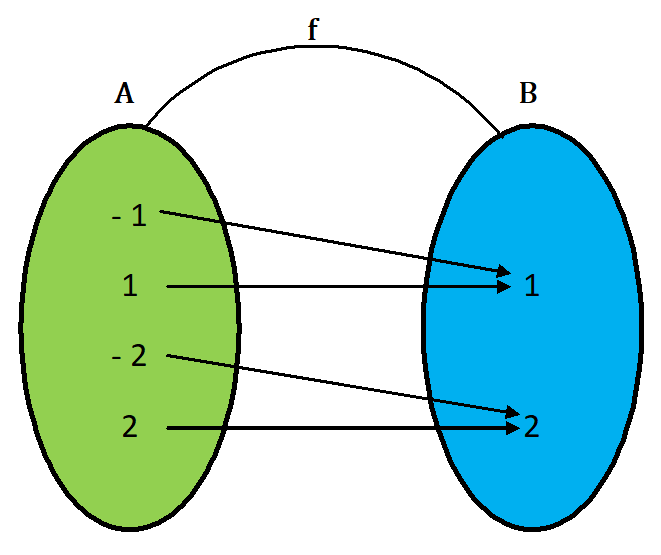
Thus, - 1 ≠ 1 but f(- 1) = f(1)
Hence, f : A → B is not one-one function.
It is a many one function