CLASS-11
OPERATION ON SETS - DIFFERENCE OF SETS
Difference Of Sets –
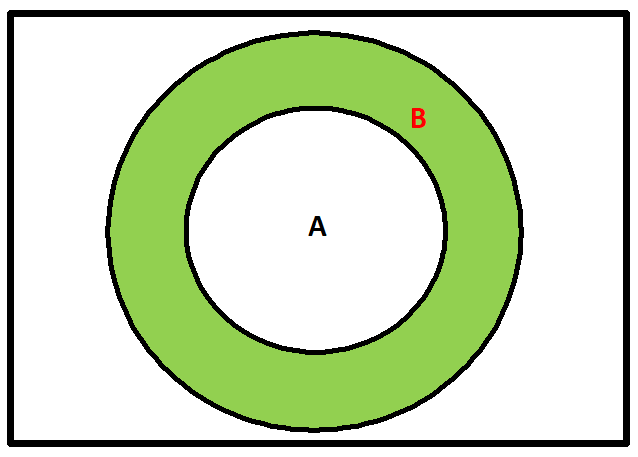
(1) Let, A and B be two sets. Then the set of all elements of A which belong to A but do not belongs to B is called the difference of sets A and B and is denoted by A – B.
(2) The set of all elements which belong to B but do not belong to A is called the difference of sets B and A and is denoted by B – A. Thus
A – B = {x ǀ x ∈ A, x ∉ B}
B – A = {x ǀ x ∈ B, x ∉ A}
For Example –
(i) Let A = {1, 2, 3, 4, 5}, B = {3, 4, 5, 6, 7},
then A – B = {1, 2}, B – A = {6, 7}
Please note, A – B ≠ B – A
(ii) Let A = {1, 3, 5, 7, 9, 11, 13, 15}, B = {3, 5, 7, 9}
then A – B = {1, 11, 13, 15}, B – A = ϕ.
Please note, A – B ≠ B – A
Please note, the difference of sets A & B is also denoted by A / B.
Example.1) If A = {3, 6, 9, 12, 15, 18, 21, 24, 27, 30}, B = {4, 8, 12, 16, 20, 24, 28, 32}, C = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24}, and D = {5, 10, 15, 20, 25, 30, 35}
(i) A – B
Ans.) A – B = {the element which are in A but not in B}
= {3, 6, 9, 12, 15, 18, 21, 24, 27, 30} – {4, 8, 12, 16, 20, 24, 28, 32}
= {3, 6, 9, 15, 18, 21, 27, 30}
(ii) A – C
Ans.) A – C = {the elements which are in A but not in C}
= {3, 6, 9, 12, 15, 18, 21, 24, 27, 30} – {2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24}
= {3, 6, 9, 15, 21, 27, 30}
(iii) A – D
Ans.) A – D = {the elements which are in A but not in D}
= {3, 6, 9, 12, 15, 18, 21, 24, 27, 30} – {5, 10, 15, 20, 25, 30, 35}
= {3, 6, 9, 12, 18, 21, 24, 27}
(iv) B – A
Ans.) B – A = {the elements which are in B but not in A}
= {4, 8, 12, 16, 20, 24, 28, 32} – {3, 6, 9, 12, 15, 18, 21, 24, 27, 30}
= {4, 8, 16, 20, 28, 32}
(v) C – A
Ans.) C – A = {the elements which are in C but not in A}
= {2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24} – {3, 6, 9, 12, 15, 18, 21, 24, 27, 30}
= {2, 4, 8, 10, 14, 16, 20, 22}
(vi) D – A
Ans.) D – A = {the elements which are in D but not in A}
= {5, 10, 15, 20, 25, 30, 35} – {3, 6, 9, 12, 15, 18, 21, 24, 27, 30}
= {5, 10, 20, 25, 35}
(vii) B – C
Ans.) B – C = {the elements which are in B but not in C}
= {4, 8, 12, 16, 20, 24, 28, 32} – {2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24}
= {20, 28, 32}
(viii) B – D
B – D = {the elements which are in B but not in D}
= {4, 8, 12, 16, 20, 24, 28, 32} – {5, 10, 15, 20, 25, 30, 35}
= {4, 8, 12, 16, 24, 28, 32}
(ix) C – B
Ans.) C – B = {the elements which are in C but not in B}
= {2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24} – {4, 8, 12, 16, 20, 24, 28, 32}
= {2, 6, 10, 14, 18, 22}
(x) D – B
Ans.) D – B = {the elements which are in D but not in B}
= {5, 10, 15, 20, 25, 30, 35} – {4, 8, 12, 16, 20, 24, 28, 32}
= {5, 10, 15, 25, 30, 35}
(xi) C – D
Ans.) C – D = {the elements which are in C but not in D}
= {2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24} – {5, 10, 15, 20, 25, 30, 35}
= {2, 4, 6, 8, 12, 14, 16, 18, 22, 24}
(xii) D – C
Ans.) D – C = {the elements which are in D but not in C}
= {5, 10, 15, 20, 25, 30, 35} – {2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24}
= {5, 15, 25, 30, 35}
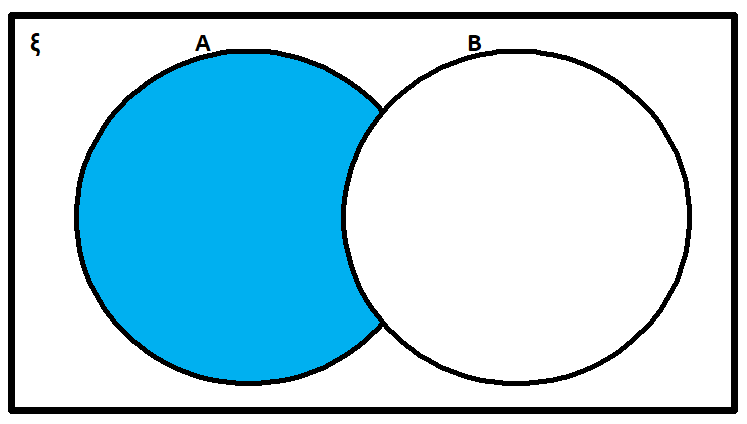
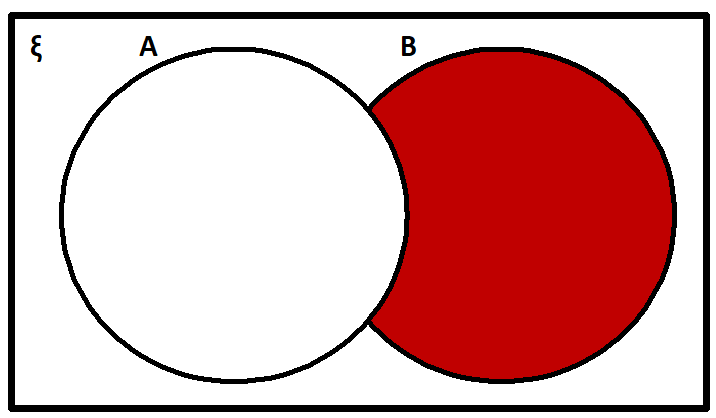
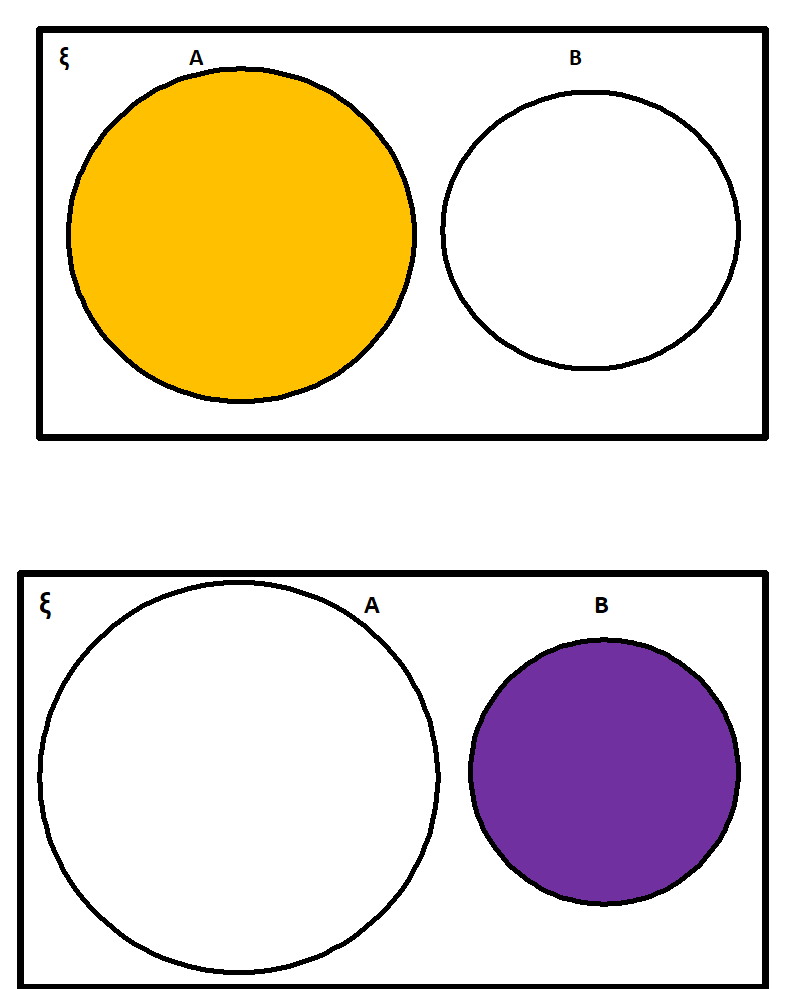
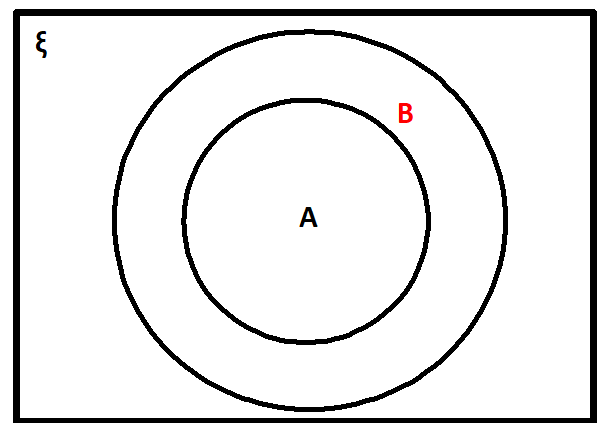
Properties Of Difference Of Sets.
Your second block of text...