CLASS-4
SOLIDS
SOLIDS -
Solids are one of the three states of matter, along with liquids and gases. In contrast to liquids and gases, solids have a fixed shape and volume that do not depend on the container in which they are placed. The particles that make up a solid are packed closely together and have a relatively low amount of energy, which causes them to vibrate in place rather than move freely.
Solids are generally characterized by their rigidity, high density, low compressibility, and inability to flow. However, there are some exceptions to these properties. For example, some solids, such as certain types of glass or plastics, can be molded or shaped when heated. Others, like some types of metals, can be bent or stretched without breaking.
Common examples of solids include rocks, metals, wood, plastic, and ice. Many everyday objects, such as chairs, tables, and buildings, are made of solids. Solids also play an important role in the field of materials science, where scientists study the properties and behavior of different types of solids to develop new materials with specific properties for a variety of applications.
Solids are a state of matter that have a definite shape and volume. They are characterized by particles that are tightly packed together and have strong intermolecular forces. Solids have a high density and are typically not compressible. They do not flow, and their shape and volume do not depend on the container in which they are placed. Examples of solids include metals, rocks, wood, plastics, and many more. Solids have a wide range of properties, including hardness, brittleness, elasticity, and conductivity, which make them useful in a variety of applications.
In physics and materials science, a solid is a state of matter characterized by the following properties:
- It has a definite shape and volume: Solids have a fixed shape and volume that do not depend on the container in which they are placed.
- It is rigid: Solids are relatively rigid, meaning they resist changes in shape or volume when subjected to external forces.
- It has a high density: The particles in a solid are densely packed together, resulting in a relatively high density compared to liquids or gases.
- It has a low compressibility: Solids are difficult to compress because the particles are already closely packed together.
- It does not flow: Unlike liquids, solids do not flow and therefore have a fixed shape.
Examples of solids include metals, rocks, wood, plastics, and many more.
In a single words, an object which occupies some space is called a solid.
Let us learn about the properties of some solids.
1. CUBOID -
¨ A cuboid has six faces, twelve edges and eight corners.
A cuboid is a three-dimensional solid shape that is bounded by six rectangular faces. It is also known as a rectangular prism. A cuboid has three pairs of parallel faces and opposite faces are congruent (i.e., they have the same size and shape). The edges of a cuboid are perpendicular to adjacent edges, and each vertex of a cuboid is the point where three edges meet.
The volume of a cuboid can be calculated by multiplying its length, width, and height. The surface area of a cuboid can be calculated by adding the areas of its six faces. The formulas for the volume and surface area of a cuboid are:
Volume = length x width x height Surface area
= 2(length x width + width x height + height x length)
Examples of objects that are shaped like a cuboid include rectangular boxes, books, bricks, and some types of buildings.
¨All its faces are flat and rectangular in shape.
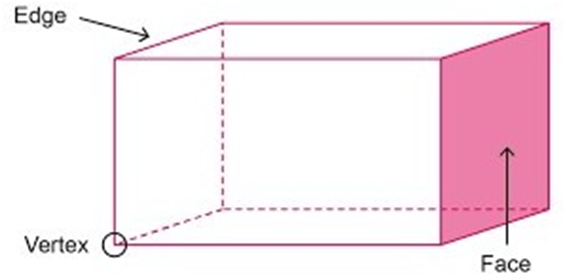
¨Examples of cuboids are brick, book, almirah.

A cuboid is a three-dimensional solid shape that is defined by six rectangular faces. It is also known as a rectangular prism. A cuboid has 12 edges, 8 vertices, and 6 faces, which are all rectangular. The opposite faces of a cuboid are congruent and parallel to each other, and each face is perpendicular to the faces adjacent to it. The volume of a cuboid can be calculated by multiplying its length by its width by its height, while its surface area can be found by adding up the areas of all its faces. Examples of objects that are roughly cuboid in shape include boxes, books, and refrigerators.
2. CUBE -
¨ A cube has six faces, twelve edges and eight corners.
¨ All its faces are flat and square in shape.
A cube is a three-dimensional solid shape that is bounded by six square faces. It is a special case of a cuboid where all six faces are squares, and all of its edges are of equal length. A cube has three pairs of parallel faces, and all of its faces are congruent (i.e., they have the same size and shape).
The volume of a cube can be calculated by the formula s³, where s is the length of an edge. The surface area of a cube can be calculated by the formula 6s², where s is the length of an edge.
Cubes have some unique properties, including:
- All edges of a cube are of equal length, and all faces are congruent squares.
- A cube has 12 edges, 8 vertices, and 6 faces.
- The diagonal of a cube is the square root of 3 times the length of an edge.
- Cubes are used in many applications, such as dice, Rubik's cubes, and storage containers.
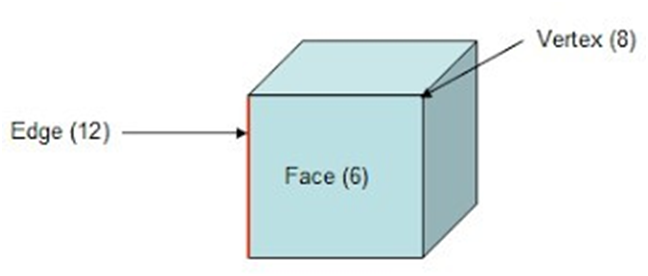
¨Examples of objects that are shaped like a cube include dice, sugar cubes, and some types of storage containers.
3. SPHERE -
A sphere is a three-dimensional solid shape that is perfectly symmetrical in all directions. It is defined as the set of all points in three-dimensional space that are at a fixed distance (called the radius) from a given point called the center. A sphere has a smooth, curved surface and is not bounded by any edges or corners.
The volume of a sphere can be calculated by the formula (4/3) x pi x r³, where r is the radius of the sphere. The surface area of a sphere can be calculated by the formula 4 x pi x r².
Spheres have some unique properties, including:
- All points on the surface of a sphere are equidistant from its center.
- The surface area of a sphere is minimized for a given volume, making it an efficient shape for storing or enclosing things.
- Spheres have high symmetry and are used in many scientific and engineering applications, such as in designing lenses, bearings, and pressure vessels.
¨ A sphere has only one curved face.
¨It does not have any edge or corner.
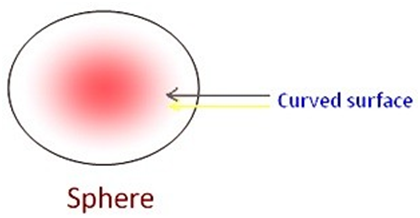
Examples of objects that are shaped like a sphere include footballs, planets, volley ball and some types of ornaments.

4. CYLINDER -
¨A cylinder has three faces- top and bottom are flat, middle is curved.
¨ It has two edges but no corner.
A cylinder is a three-dimensional solid shape that has two parallel, congruent circular bases connected by a curved surface. It is a type of prism, and its cross-section is always the same shape as its base. A cylinder has a curved surface area, two congruent circular bases at the top and bottom, and a fixed height between the bases.
The volume of a cylinder can be calculated by the formula pi x r²x h, where r is the radius of the circular base and h is the height of the cylinder. The surface area of a cylinder can be calculated by the formula 2pi x r²+ 2pi x r x h, where r is the radius of the circular base and h is the height of the cylinder.
Cylinders have some unique properties, including:-
- All points on the circular bases of a cylinder are equidistant from its axis of symmetry.
- A cylinder can be thought of as a stack of circular disks or a curved version of a rectangle.
- Cylinders are used in many applications, such as cans, pipes, and some types of containers.
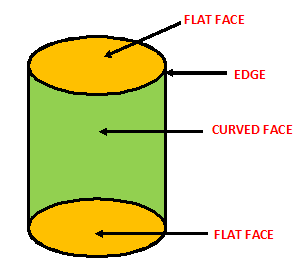
¨Example of cylinder is road-roller.

5. CONE -
¨ A cylinder has two faces- bottom face is flat and the other face is curved.
A cone is a three-dimensional geometric shape that has a circular base and tapers smoothly to a point or vertex at the top. It is a type of pyramid, but unlike a square or rectangular pyramid, a cone has a circular base. The distance from the vertex to any point on the circular base is called the height of the cone, and the radius of the circular base is called the base radius. The volume of a cone can be calculated by using the formula (1/3)πr²h, where r is the radius of the circular base and h is the height of the cone. The surface area of a cone can be calculated using the formula πr²+ πr√(r²+ h²), where r is the radius of the circular base and h is the height of the cone. Cones have many real-world applications, such as in traffic cones, ice cream cones, and volcanic cones.
A cone is a three-dimensional geometric shape that consists of a circular base, a curved surface that tapers to a point called the apex, and a height that measures the distance from the apex to the base. A cone can be classified as a right cone or an oblique cone depending on whether the axis of the cone is perpendicular to its base or not. Cones are commonly found in many areas of science and engineering, such as in the construction of traffic cones, ice cream cones, and the cones of volcanoes. The volume of a cone can be calculated using the formula V = (1/3)πr²h, where V is the volume, r is the radius of the base, and h is the height. The lateral surface area of a cone can be calculated using the formula L = πrℓ, where L is the lateral surface area, r is the radius of the base, and ℓ is the slant height of the cone, which is the distance from the apex to any point on the edge of the base.
¨ It has one edge and one corner.
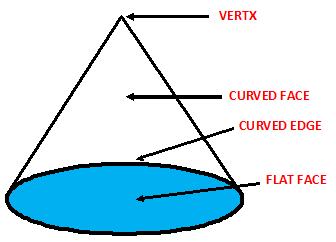
¨ Example of cone is joker’s cap, ice-cream cone.
