CLASS-4
PERIMETER OF A RECTANGLE
PERIMETER OF A RECTANGLE -
As we all know that, a rectangle is a four sided figure, and Its opposite sides are equal.
The longer side is known as length and the shorter side is known as breadth/ width.
Perimeter of a rectangle = (length + breadth) x 2

Example.1) Find the perimeter of a rectangle
whose length is 1.85 cm and breadth is 2.20 cm.
Ans.)
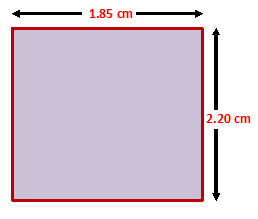
Length = 1.85 cm
Breadth = 2.20 cm
∴ Perimeter of a rectangle=
= (length + breadth) x 2
= (1.85 cm + 2.20 cm) x 2
= 4.05 cm x 2
= 8.10 cm
Ans:The perimeter of the rectangle is 8.10 cm. (Ans.)
Example.2) The perimeter of a rectangle is 60 m. Find the breadth of the field if its length is 18 m.
And.) Perimeter of the rectangle 60 m, and length is 18 m
As we know that, perimeter of the rectangle = 2 (Length + Breadth)
So, 60 = 2 (Length + Breadth)
=> (Length + Breadth) = 30
=> 18 + Breadth = 30
=> Breadth = 30 - 18 = 12
So, the required breadth is 12 m (Ans.)
Example.3) If the length of the rectangular garden is thrice its breadth and if the breadth is 15 m find the perimeter of the garden
Ans.) Let, Length = L, and Breadth = B
As per the given condition, length of the rectangular garden is thrice its breadth, so L = 3 B and B = 15 m
Now, perimeter of rectangle is = 2 (Length + Breadth)
= 2 (L + B)
= 2 (3 B + B) [where L = 3 B]
= (2 X 4 B)
= 8 B
= (8 X 15) [where B = 15 m]
= 120 m
Now, as per the condition -
Perimeter of Rectangle is = 2 (Length + Breadth)
So, 120 m = 2 (Length + Breadth)
Length + Breadth = 60 m
Now, Length + 15 m = 60 m
so, Length = 60 m - 15 m = 45 m
Or,
L = 3 B = (3 X 15)
L = 45 m
So, the length and perimeter of the rectangle is 45 m and 120 m respectively. (Ans.)