CLASS-4
LCM - PRIME FACTORIZATION METHOD
FINDING LCM Via PRIME FACTORIZATION METHOD -
PRIME FACTORIZATION METHOD : TWO NUMBERS -
In this method USE PRIME NUMBERS ONLY
§ STEP 1.) First we find the prime factors of the given numbers separately by factorization using the prime numbers.
§ STEP 2.) Then we underline the common prime factors of the numbers and write it down.
§ STEP 3.) Next we write the other factors of all numbers also.
§ STEP 4.) The product of these common prime factors and the other factors is the L.C.M of the given numbers.
Example.) Find the L.C.M of 144 and 360 using the prime factorization method. SOLUTION: (USE PRIME NUMBERS ONLY)
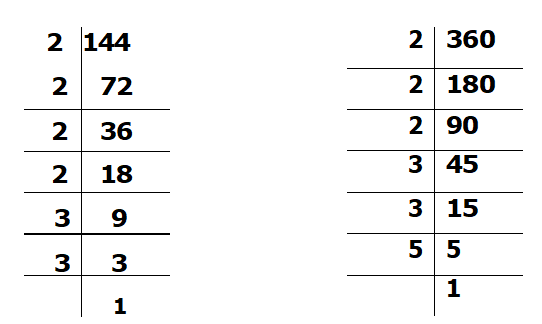
STEP 1.
144 = 2 x 2 x 2 x 2 x 3 x 3
(Write the prime factors and color pink the common factors)
360 = 2 x 2 x 2 x 3 x 3 x 5
STEP 2.
LCM = 2 x 2 x 2 x 3 x 3 x 2 x 5
(Multiply the common factors and the other factors also)
STEP 3.
L.C.M = 720 (The product is the L.C.M)
STEP 4.
Answer: The LCM of 144 and 360 is 720. (Ans.)
LCM : PRIME FACTORIZATION METHOD :(THREE NUMBERS) -
Example.) Find the LCM of 12, 15 and 20 using prime factorization method. (USE PRIME NUMBERS ONLY)
Ans.)
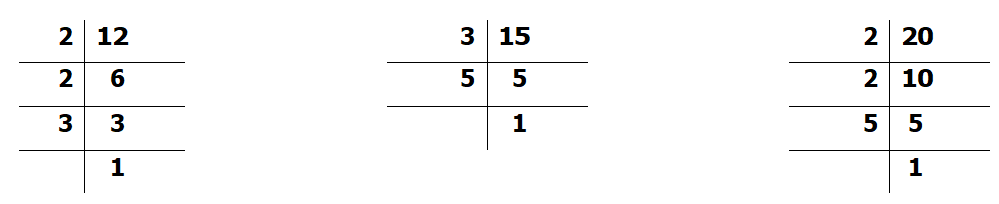
12 = 2 x 2 x 3
15 = 3 x 5
20 = 2 x 2 x 5
L.C.M = 2 x 2 x 3 x 5 = 60
Ans: The LCM of 12, 15 and 20 is 60. (Ans.)