CLASS-5
DIVISION OF FRACTION
DIVISION OF FRACTION
Before understand the process of Division we have to understand ‘Reciprocal’ or ‘Multiplicative Inverse’ first. ‘Reciprocal’ or ‘Multiplicative Inverse’ of a fraction is nothing but obtained by interchanging of ‘Numerator’ and ‘Denominator’ or inverting of the given fraction.
Suppose there is a fraction, that is 3/5, but via inverting it becomes 5/3 and it is called ‘Reciprocal’ of ‘Multiplicative Inverse’
There are some example are given below to understand the relation between Original fraction and Reciprocal or Multiplicative Inverse –
Original Fraction Multiplicative Inverse OR Reciprocal
5 8
1) ------- (Proper fraction) --------- (Improper fraction)
8 5
9 7
2) -------- (Improper fraction) --------- (Proper Fraction)
7 9
3 1
3) 3 (whole number) = -------- -------- (proper fraction)
1 3
1 1
4) 1 = -------- -------- = 1
1 1
3 23 5
5) 4 ------ = ------- (Complex/Mix Number) ------- (proper fraction)
5 5 23
6) 0 0 (don’t have any reciprocal)
Division Of Whole Numbers by a Fraction
1) Find the number of 1/4 in 2.
1
Ans.) Number of 1/4 in 2 = 2 ÷ -------
4
2 4 2 x 4
= -------- x -------- = ----------
1 1 1 x 1
8 [Change the divisor to reciprocal or
= ---------- = 8 (Ans.) multiplicative inverse and also change
1 from ( ÷ ) division sign to multiplication ( x ) sign.]
2) Find the number of 1/10 in 5.
1
Ans.) Number of 1/10 in 5 = 5 ÷ -------
10
5 10 10 x 5
= ------- x -------- = -----------
1 1 1 x 1
50 [Change the divisor to reciprocal or
= ---------- = 50 (Ans.) multiplicative inverse and also
1 change from (÷) division sign to multiplication (x) sign.]
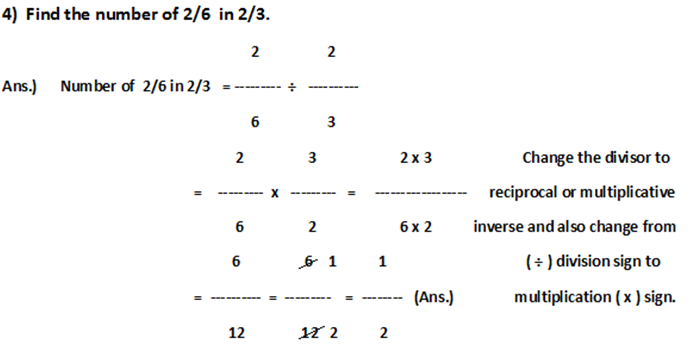
3) Find the number of 1/8 in 4/15.
1 4
Ans.) Number of 1/8 in 4/15 = -------- ÷ ---------
8 15
1 15 1 x 15
= ------- x -------- = ------------
8 4 8 x 4
15 [Change the divisor to reciprocal or
= ---------- (Ans.) multiplicative inverse and also change
32 from (÷) division sign to multiplication (x) sign.]