CLASS-5
ARRANGING FRACTION IN ASCENDING ORDER
ARRANGING FRACTION IN ASCENDING ORDER -
To arrange fractions in ascending order, we need to find a common denominator for all the fractions and then compare the numerators. Here's a step-by-step guide:
- Identify the fractions that need to be arranged in ascending order.
- Find the least common multiple (LCM) of the denominators of all the fractions. This will be the common denominator.
- Convert each fraction to an equivalent fraction with the common denominator. To do this, multiply the numerator and denominator of each fraction by the same number that will make the denominator equal to the LCM.
- Compare the numerators of the fractions and arrange them in ascending order.
- If any of the fractions are mixed numbers, convert them to improper fractions before proceeding.
Arrange the following fractions in ascending order: 1/3, 2/5, 4/15, 1/6
- The fractions are 1/3, 2/5, 4/15, 1/6.
- The LCM of the denominators is 30.
- Convert each fraction to an equivalent fraction with the common denominator of 30, 1/3 = 10/30, 2/5 = 12/30, 4/15 = 8/30, 1/6 = 5/30.
- Compare the numerators and arrange the fractions in ascending order: 5/30, 8/30, 10/30, 12/30.
- Convert the improper fractions back to mixed numbers if necessary: 5/30 = 1/6, 8/30 = 4/15, 10/30 = 1/3, 12/30 = 2/5.
Therefore, the fractions arranged in ascending order are: 1/6, 4/15, 1/3, 2/5.
To arrange fractions in ascending order, we need to find a common denominator for all the fractions. Once we have a common denominator, we can compare the numerators and arrange the fractions accordingly. Here are the steps to arrange fractions in ascending order:
- Find the least common multiple (LCM) of the denominators of all the fractions.
- Convert each fraction to an equivalent fraction with the LCM as the denominator.
- Compare the numerators of the fractions and arrange them in ascending order.
Let's take an example to understand this better. Suppose we have to arrange the fractions 1/3, 2/5, and 4/15 in ascending order.
- The LCM of the denominators 3, 5, and 15 is 15.
- Convert each fraction to an equivalent fraction with 15 as the denominator:1/3 = 5/15, 2/5 = 6/15, 4/15 = 4/15, (already in the correct form)
- Now, compare the numerators of the fractions: 4/15, 5/15, 6/15. The fractions are already in ascending order, so we don't need to do anything else.
Therefore, the fractions arranged in ascending order are:
4/15, 5/15, 6/15.
Simplifying the fractions gives:
4/15, 1/3, 2/5.
So, now we come to know that the basic rules for arranging fraction into ascending order -
First find the L.C.M. Then form equivalent fractions such that the denominators are equal to the L.C.M. Then write in ascending order comparing the numerators.
Example.1) Arranging Following fraction in ascending order -
7 5 2
-------, -------, -------
24 12 3
Ans.)
Now, we would like to find the LCM of all the denominator of given fraction, and then we will divide obtained LCM by every denominator of given fraction one by one and then will multiply numerator and denominator by obtained quotient and make equalize all the denominator of the given fraction.
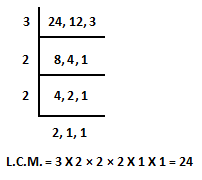
7 7 × 1 7
------- = ---------- = ------- [24 (LCM) ÷ 24 = 1]
24 24 × 1 24
5 5 × 2 10
------- = --------- = -------- [24 (LCM) ÷ 12 = 2]
12 12 × 2 24
2 2 × 8 16
------ = --------- = -------- [24 (LCM) ÷ 3 = 8]
3 3 × 8 24
7 10 16
------ < ------- < -------
24 24 24
(as 7 < 10 < 16)
The fractions arranged in ascending order :
7 5 2
------- < ------- < ------- (Ans.)
24 6 3
Example.2) Arranging Following fraction in ascending order -
5 4 7
-------, -------, -------
9 27 18
Ans.)
Now, we would like to find the LCM of all the denominator of given fraction, and then we will divide obtained LCM by every denominator of given fraction one by one and then will multiply numerator and denominator by obtained quotient and make equalize all the denominator of the given fraction.
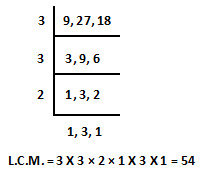
5 9 × 5 45
------- = ---------- = ------- [54 (LCM) ÷ 9 = 6]
9 9 × 6 54
4 4 × 2 8
------- = ---------- = -------- [54 (LCM) ÷ 27 = 2]
27 27 × 2 54
7 7 × 3 21
------- = --------- = ------- [54 (LCM) ÷ 18 = 3]
18 18 × 3 54
8 21 45
-------, --------, --------
54 54 54
(as 8 < 21 < 45)
The fractions arranged in ascending order :
4 7 5
------- < ------- < ------- (Ans.)
27 18 9