CLASS-5
DIVISION IN MEASUREMENT

DIVISION IN MEASUREMENT -

Division is an arithmetic operation that can also be applied to measurements, but similar to other operations, it requires careful consideration of units and dimensions to ensure the validity and meaningfulness of the result.

When dividing two measurements with the same unit and dimension, the process is straightforward. You simply divide the numerical values. For example, if you have a distance of 12 meters and you want to divide it by 3, the result would be 4 meters.

However, when dealing with measurements that have different units or dimensions, additional conversions are necessary before division can be performed.

For instance, let's say you want to divide a distance in meters (e.g., 9 meters) by a distance in centimeters (e.g., 300 centimeters). To perform the division, you need to convert one of the measurements to match the other. Converting 300 centimeters to meters by dividing by 100 gives you 3 meters. Now, you can divide 9 meters by 3 meters to get a result of 3.

When dividing measurements with different dimensions, the result may have a different dimension or interpretation altogether.

For example, if you divide a volume of 8 cubic meters by a length of 2 meters, the resulting quotient would have the dimension of cubic meters divided by meters, which would yield a cross-sectional area of 4 square meters.

Always consider the units and dimensions involved when dividing measurements. Ensure that the measurements are of the same type or have been appropriately converted to a common unit or dimension to obtain a meaningful result.

Division is another arithmetic operation that can be applied to measurements, but it requires careful consideration of units and dimensions to ensure the validity and meaningfulness of the result.

When dividing two measurements with the same unit, the process is straightforward. You simply divide the numerical values. For example, if you have a distance of 12 meters and you divide it by a time of 3 seconds, the result would be a speed of 4 meters per second.

However, when dealing with measurements that have different units or dimensions, additional conversions are necessary before division can be performed.

For instance, if you want to divide a distance in meters (e.g., 20 meters) by a time in seconds (e.g., 5 seconds), no additional conversion is needed. You can simply divide 20 meters by 5 seconds to get a result of 4 meters per second.

When dividing measurements with different dimensions, such as dividing a volume by a length, it's important to understand the meaning and implications of the operation. The result may have a different dimension or interpretation altogether.

For example, if you divide a volume of 15 cubic meters by a length of 3 meters, the resulting quotient would have the dimension of cubic meters divided by meters, which would yield an area of 5 square meters.

Always consider the units and dimensions involved when dividing measurements. Ensure that the measurements are of the same type or have been appropriately converted to a common unit or dimension to obtain a meaningful result.

While doing Division in Measurement we have to express the given measures in the same unit by using the decimal notation and then do Division as in the case of decimals. But before doing that we need to arrange the given units in their place value chart, putting the digits in their proper places, taking the vacant places as zero.

Express in decimal notation and then divide:-

a)  591 kg 7 hg 3 dag 6 g by 68

       kg    hg   dag    g

      591   7     3     6   =   591.736 kg

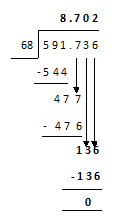
Answer is 8.702 kg     (Ans.)

b)  936 kl 312l by 39 [Answer in litres]

   kl        hl      dal       l

  936       3       1        2    =   936.312  kl

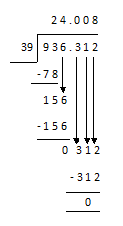
24.008 kl

1 kl = 1000 l

24.008 kl = 24 × 1000 = 24008 l

Answer is 24008 l       (Ans.)