CLASS-6
ADDITION OF ALGEBRAIC EXPRESSION IN LIKE TERM
ADDITION OF ALGEBRAIC EXPRESSION IN LIKE TERM -
When adding algebraic expressions with like terms, you combine the coefficients of the like terms while keeping their variables and exponents unchanged. Like terms are terms that have the same variables raised to the same powers. Here are the steps to add algebraic expressions with like terms:
1. Identify Like Terms:- First, identify the like terms in the expressions. Like terms are terms that have the same variables with the same exponents.Example: Let's say you want to add the following two expressions:
Expression 1:- 3x²+ 2y - 5x - 3
Expression 2:- - x²+ 4y + 7x + 5
In this case, the like terms are:- 3x² and - x²(both have "x" raised to the second power)
2y and 4y (both have "y" as a first-degree term)
- 5x and 7x (both have "x" as a first-degree term).
2. Group Like Terms:- Group the like terms together. In this case, you'll have one group for the quadratic terms, one for the linear terms, and one for any constant terms.
3. Combine Coefficients:- For each group of like terms, combine the coefficients (the numerical parts) by performing addition or subtraction as needed.
For the "x²" terms: 3x²- x² = 2x²
For the "y" terms: 2y + 4y = 6y
For the "x" terms: -5x + 7x = 2x
4. Combine Constants:- If there are any constant terms in the expressions, add or subtract them.
- In the example expressions, the constants are "-3" and "5." Add them: -3 + 5 = 2.
5. Write the Result:- Write down the combined like terms along with any other terms that are not like terms. This represents the sum of the two expressions. Sum:- 2x²+ 6y + 2x + 2
So, the sum of the two given expressions is "2x²+ 6y + 2x + 2."
Example 1.) Adding Like Terms
Given the expressions:
- 3x²+ 2x - 5
- 2x²+ 4x + 1
Ans.)
Identify and add the like terms:
- 3x²+ 2x - 5
- 2x²+ 4x + 1
(3x²+ 2x²) + (2x + 4x) + (-5 + 1)
Now, combine the like terms:
- 5x²+ 6x - 4
So, the simplified expression is 5x²+ 6x - 4. (Ans.)
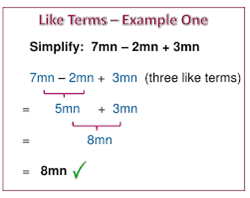
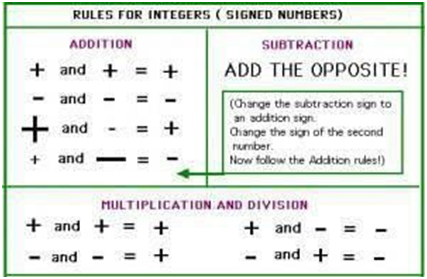
When adding algebraic expressions with like terms, it's essential to be organized and systematic in identifying and combining the like terms. Remember that you only combine terms that have the same variables with the same exponents, and you leave other terms as they are.