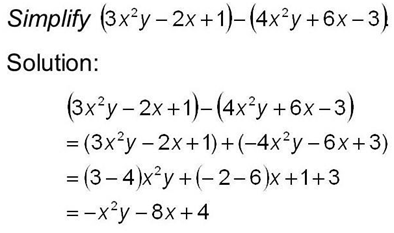CLASS-6
SUBTRACTION OF ALGEBRAIC EXPRESSION - HORIZONTAL METHOD

SUBTRACTION OF ALGEBRAIC EXPRESSION (HORIZONTAL METHOD) -

Subtracting algebraic expressions horizontally involves writing the terms of the expressions in a horizontal line and then performing subtraction. This method is particularly useful when you have to subtract algebraic expressions with multiple terms. Here are the steps for subtracting algebraic expressions horizontally:

Step 1:- Write the Expressions Horizontally

Write the two expressions one below the other horizontally, ensuring that like terms are aligned vertically.

For example, let's subtract Expression B from Expression A:

Expression A:   4x²- 3xy + 2y

Expression B:   2x²+ 5xy - y

Step 2:- Distribute the Subtraction Sign

Distribute the subtraction sign to each term in Expression B. This means changing the sign of every term in Expression B to its opposite (positive to negative or negative to positive).

Expression A:    4x²- 3xy + 2y

Expression B:   -(2x²+ 5xy - y)

Step 3:- Align Like Terms Vertically

Arrange the terms vertically, aligning like terms under each other. This makes it easier to subtract like terms.          

      4x² - 3xy + 2y

    -(2x²+ 5xy - y)

---------------------

Step 4:- Perform Subtraction

Now, subtract the coefficients of the like terms vertically. Remember to retain the variable parts unchanged.

• For "4x²- 2x²," subtract the coefficients: 4x²- 2x²= 2x².
• For "-3xy - 5xy," subtract the coefficients: -3xy - 5xy = -8xy.
• For "2y - (-y)," subtract the coefficients: 2y - (-y) = 2y + y = 3y.

Step 5:- Write the Result

Write down the result of the subtraction, combining the simplified terms:

 2x²- 8xy + 3y

So, the simplified result of subtracting Expression B from Expression A horizontally is:

 2x²- 8xy + 3y.

This method helps you organize the terms neatly and subtract them systematically, especially when dealing with complex algebraic expressions with multiple terms.