CLASS-6
EXPONENTS

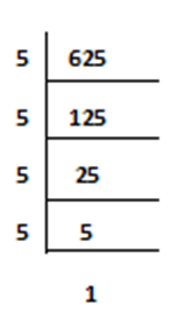
Step.1)  First find the prime factorization of the given number.

Step.2)  After completing prime factorization of the given number observe how many base has come with their exponents. Clearly shown that only 5 has come 4 times .

Step.3) Clearly shown that 5 has come 4 times, so 5 is the base and 4 its exponents.

       So, it can be written as 5⁴.

     625 =  5 x 5 x 5 x 5 = 5⁴.    (Ans.)

5) Write 38880 in exponential form.

Step.1)  First find the prime factorization of the given numbers.

Step.2)  After completing prime Factorization of the given number observe how many base and their exponents we can find.

Step.3) Clearly shown that 2 has come 5 times, 5 has come 1 time and 3 has come 5 times. so it can be written as 5⁴.

Step.4) 2 has come 5 times, so 2 is base 5 its exponent. It can be written 2⁵. 5 has come 1 time, so 5 is base and 1 its exponent. It can be written 5¹. 3 has come 5 times, so 3 is base and 5 its exponent. It can be written 3⁵.

Step.5.) Exponential form can be written as multiplication of base with their exponents like 

2⁵ x 5¹ x 3⁵ 

38880 = 2 x 2 x 2 x 2 x 2 x 5 x 3 x 3 x 3 x 3 x 3

= (2 x 2 x 2 x 2 x 2) x 5 x (3 x 3 x 3 x 3 x 3) 

= 2⁵ x 5¹ x 3⁵  (Ans.)

6)  Write the product of number 3ᶟ and 3⁵ as single power.

Ans.)   3ᶟ and 3⁵                             

     =  3ᶟ x  3⁵ =  3 ᶟ⁺⁵ =  3⁸

Step.1)  Observe the given two-digit, where the base are the same but exponents are different.

Step.2)  We follow the rules- 

If ‘A’  is any number and let x & y are the natural numbers,

             then-  Aˣ x Aʸ  =  A⁽ˣ⁺ʸ⁾

    3⁸ =  3 x 3 x 3 x 3 x 3 x 3 x 3 x 3 = 6561    (Ans.)

7)  Write the product of number (-8)⁵ and (-8)⁷ as single power.

Ans.)   (-8)⁵ and (-8)⁷                            

     =  (-8)⁵ x (-8)⁷ =  (-8) ⁵⁺⁷ =  (-8)¹² 

Step.1)  Observe the given two-digit, where the base are the same but exponents are different.

Step.2) We follow the rules- If ‘A’ is any number and let x & y are the natural numbers,

         then-  Aˣ  x  Aʸ  =  A⁽ˣ⁺ʸ⁾

= (-8) x (-8) x (-8) x (-8) x (-8) x (-8) x (-8) x (-8) x (-8) x  (-8) x (-8) x (-8)

     =  (- 68719476736)  (Ans.)

8)  Evaluate   (3⁴)²

   (3⁴)²  =  (3)⁴˟² =  3⁸

 Step.1) We can observe that, there is one base two exponents

 Step.2)   We will follow the rules –

      If ‘A’ is any number, m & n are the natural number, then-

                     ( Aᵐ) ⁿ =   Aᵐⁿ

  3⁸ =   3 x 3 x 3 x 3 x 3 x 3 x 3 x 3  = 6561   (Ans.)

9)  Multiply 5⁴ and  2⁴

Ans.)   5⁴ and  2⁴ =  5⁴  x  2⁴  =  10⁴                               

Step.1) We can observe that, in given numbers base are different but exponents are equal.   

Step.2) we follow the rules as discussed below -                       

If ‘A’ & ‘B’ are any number and m is a natural number, then

                   Aᵐ  x  Bᵐ  =  (AB)ᵐ

           =  10⁴  =  10 x 10 x 10 x 10 

                                  =  10000           (Ans.)

10) Explain (-5)⁵ = ?                                       

Ans.)  (-5)⁵                

    =  (-5) x (-5) x (-5) x (-5) x (-5)

    = - 3125     (Ans.)

Step.1) Here we can observe that there are single base and the exponents are shown 5 times, so we have to multiply the given base by 5 times.

Step.2) Value comes with a negative (-) sign or value because - 

as pr rules (-A)ᵐ = - Aᵐ when ‘m’ is odd. 5 is odd number

(-5) x (-5) x (-5) x (-5) x (-5) = - 3125  

             So , -3125 is the actual/final result.     (Ans.)

11)  Evaluate  9⁷ / 9⁴

Ans.)    9⁷ / 9⁴

        9⁷     

 = ---------   =    9⁷⁻⁴   =   9ᶟ 

        9⁴         

Step.1) Observe in a given fraction base are the same but exponents are different. so

Step.2) We follow the rules -

If ‘A’ is any number, m & n are the natural number, where m > n then-                         

          Aᵐ

     ----------  =  A ⁽ᵐˉⁿ⁾

          Aⁿ

 =  9ᶟ  =  9 x 9 x 9   =    729     (Ans.)