CLASS-6
PRIME FACTORIZATION

PRIME FACTORIZATION -

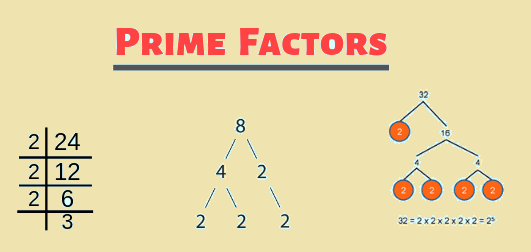
Prime factorization is a process of expressing a positive integer as a product of its prime factors. Prime factors are the prime numbers that divide the given integer without leaving any remainder.

Here's how you can find the prime factorization of a number:

  1. Start with the smallest prime number, which is 2.
  2. Divide the given number by 2. If it's divisible, write down the factor 2 and continue dividing the result by 2 until you can no longer divide evenly.
  3. Move on to the next prime number, which is 3, and repeat the division process.
  4. Continue this process with each successive prime number until the quotient becomes 1.
  5. Write down all the prime factors that you found in step.2 to step.4.
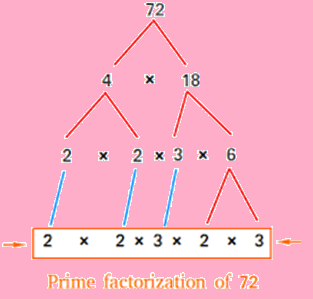
Factors
Factors
Factors

For example, let's find the prime factorization of the number 72:-

  1. Start with the smallest prime, 2.
  2. 72 ÷ 2 = 36. Write down the factor 2.
  3. 36 ÷ 2 = 18. Write down the factor 2.
  4. 18 ÷ 2 = 9. Write down the factor 2 again.
  5.  9 ÷ 3 = 3. Write down the factor 3.
  6.  3 ÷ 3 = 1. Write down the factor 3.

So, the prime factorization of 72 is 2^3 × 3^2, which means 72 can be expressed as the product of 2 raised to the power of 3 and 3 raised to the power of 2.

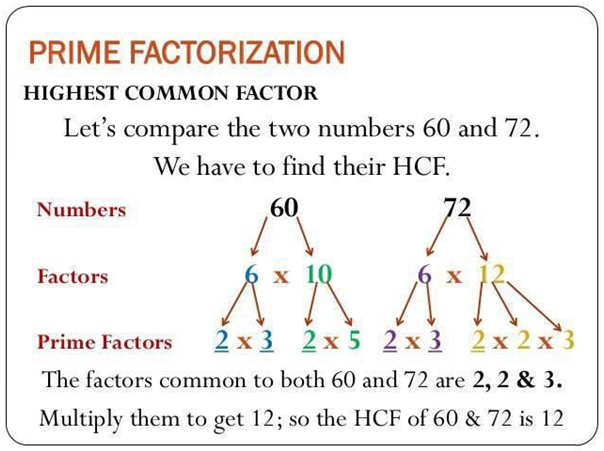
For example, let's find the prime factorization of the number 60:-

  1. Start with the smallest prime, 2.
  2. 60 ÷ 2 = 30. Write down the factor 2.
  3. 30 ÷ 2 = 15. Write down the factor 2.
  4. 15 ÷ 3 = 5. Write down the factor 3.
  5. 5 ÷ 5 = 1. Write down the factor 5.

So, the prime factorization of 60 is 2^2 × 3 × 5, which means 60 can be expressed as the product of 2 raised to the power of 2, 3 raised to the power of 1, and 5 raised to the power of 1.



Another example: Let's find the prime factorization of 126:-

  1. Start with the smallest prime, 2.
  2. 126 ÷ 2 = 63. Write down the factor 2.
  3. 63 ÷ 3 = 21. Write down the factor 3.
  4. 21 ÷ 3 = 7. Write down the factor 3.
  5. 7 is a prime number, so write it down.

The prime factorization of 126 is 2 × 3^2 × 7.

Prime factorization is useful in various mathematical contexts, such as simplifying fractions, finding the greatest common divisor (GCD), and solving certain types of equations.