CLASS-6
ANGLES AT A POINT
ANGLES AT A POINT -
When multiple rays or line segments emanate from a single point, the angles formed at that point are known as angles at a point. Specifically, these angles share a common vertex, which is the point of origin for the rays or line segments. The sum of all the angles at a point is always 360∘. Here are a couple of important concepts related to angles at a point:
- Interior Angles at a Point:-The interior angles at a point are the angles formed by two rays or line segments that share a common vertex, and these angles lie on the same side of the lines formed by the rays.The sum of all the interior angles at a point is 360∘.
- Exterior Angles at a Point:-The exterior angles at a point are the angles formed by one ray or line segment and the extension of another ray or line segment that shares a common vertex. These angles lie on opposite sides of the lines formed by the rays.The sum of all the exterior angles at a point is also 360∘.
- Adjacent Angles at a Point:- Adjacent angles at a point are pairs of angles that share a common vertex and a common side but do not overlap.The sum of adjacent angles at a point is 360∘.
4. Angles at a point :-
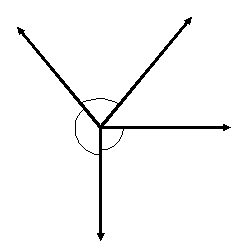
In the adjoining diagram, the four angles together make one complete turn, so they add upto 360∘. This is true no matter how many angles are formed at a point. Thus -
Sum of angles at a point = 360∘
5. Angles on one side of a straight line :-
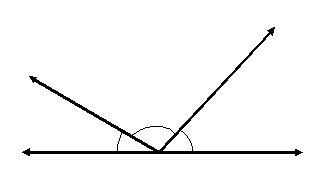
In the adjoining diagram, the three angles together make a straight angle , so they add upto 180∘
This is true no matter how many angles make up the straight line.
Thus -
Sum of angles at a point on one side of a straight line = 180∘
6. Angles making a right angle :-
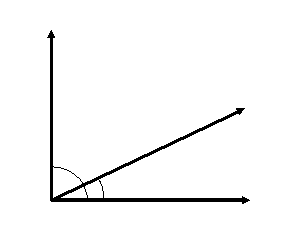
In the adjoining diagram,two angles together make a right angle, so they add upto 90∘.
This is true no matter how many angles make up the right angle. Thus -
Sum of angles in a right angle = 90∘
7. Vertically opposite angle :-
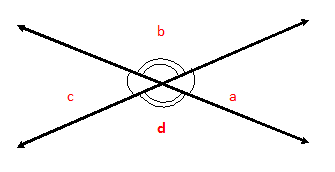
When two straight lines intersect each other, they form four angles at their point of intersection say a, b, c, and d.
Angles a & c are called vertically opposite angles to each other and so are angles b & d.
They are called vertically opposite angles because they have the same vertex and are opposite to each other.
8) Example:- Suppose you have three rays emanating from a point. The angles formed between these rays are the interior angles at the point. If these angles measure 60∘, 90∘, and 210∘, respectively, then the sum of these interior angles at the point is 60∘ + 90∘ + 210∘ = 360∘ .
Understanding angles at a point is fundamental in geometry, and this concept is frequently used when dealing with polygons, circles, and other geometric figures.