CLASS-6
CONSTRUCTION OF BISECTOR OF AN ANGLE

CONSTRUCTION OF BISECTOR OF AN ANGLE -

To construct the bisector of an angle, follow these steps:-

1. Draw the Angle:- Start by drawing the angle you want to bisect. Label the two rays that form the angle as AB and AC, where A is the vertex of the angle. 
2. Place the Compass on the Vertex:- Using a compass, place the needle at point A (the vertex of the angle).
3. Draw an Arc:- With the compass set to any radius greater than half the length of AB (or AC), draw an arc that intersects both rays of the angle. Label the points of intersection as D and E.
4. Place the Compass on D (or E):- Without changing the compass width, place the needle of the compass on point D (or E).
5. Draw an Arc:- Draw an arc that cuts the previously drawn arc inside the angle. Label the point of intersection with the original arc as F.
6. Repeat the Process:- Without changing the compass width, place the needle of the compass on point F and draw another arc similar to the one drawn in step 5. Label the point of intersection with the original arc as G.
7. Draw the Bisector:- Use a ruler or straightedge to draw a straight line connecting point A to point G. This line AG is the bisector of the angle ∠BAC.

Other Way Of Understanding -

Let ∠AOB be a given angle whose measure is not known. We want to draw the bisector of ∠AOB.

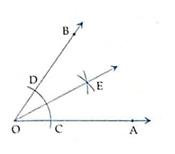
Steps Of Constructions -

Step.1) With O as centre and any (suitable) radius, draw an arc to meet ray OA at C and ray OB at D.

Step.2) With C as centre and any suitable radius (not necessarily equal to radius of step 1 > 1/2 CD), draw an arc. Also, with D as centre and same radius draw another arc to meet the previous arc at E.

Step.3) Join OE and produce it to form a ray, then ray OE is the required bisector of ∠AOB.