CLASS-6
CONSTRUCTION OF PERPENDICULAR TO A LINE AT A POINT ON THE LINE
CONSTRUCTION OF PERPENDICULAR TO A LINE AT A POINT ON THE LINE -
Constructing a perpendicular to a line at a point on the line is a fundamental geometric construction. Here's how you can do it using a straightedge and a compass:
Let's say you have a line ℓℓ and a point P on that line, and you want to construct a line perpendicular to ℓℓ passing through point P.
- Draw the given line ℓℓ and mark the point P on it.
- Place the compass on point P:- Put the compass needle on point P.
- Adjust the compass width:- Adjust the compass to a width that is longer than half the length of the line segment you want to construct. This will ensure that the arcs you draw intersect the line on both sides of point P.
- Draw two arcs:- With the compass set at the adjusted width, draw arcs above and below the line ℓℓ. Ensure that the arcs intersect the line on both sides of point P. Label these intersection points as A and B.
- Draw a straight line through points A and B:- Using a straightedge, draw a line passing through points A and B. This line will be perpendicular to line ℓℓ at point P.
Now, you've successfully constructed a line perpendicular to ℓℓ at point P.
The reasoning behind this construction lies in the fact that a perpendicular line creates right angles with the original line. By using arcs with a compass and ensuring they intersect the line on both sides of the point, you create two points that are equidistant from P. Drawing a line through these points then naturally forms a perpendicular line.
Another Way Of Understanding -
To draw a perpendicular to a line at a point on the line.
Given:- A line AB and a point P on it.
Required:- To draw a perpendicular to AB at the point P.
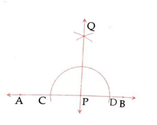
Steps Of Construction:-
Step.1) With P as centre and any suitable radius, draw an arc to cut the line AB at points C & D.
Step.2) With C & D as centres, draw two arcs of equal radius (>1/2 CD) cutting each other at Q.
Step.3) Draw a line passing through points P & Q, then QP is the required line perpendicular to the line AB at the point P.