CLASS-6
GEOMETRY-ANGLE-PROBLEM & SOLUTION

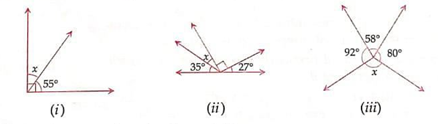
Ans.) (i) As the sum of the angles in a right angle is 90⁰,

As per the condition,

    x + 55⁰ = 90⁰

=>  x = 90⁰ - 55⁰ = 35⁰

So the angle is 35⁰ .................(Ans.)

(ii) As the sum of angles at a point on one side of a straight line = 180⁰

As per the condition,

       27⁰ + 90⁰ + x + 35⁰ = 180⁰

=>     152⁰ + x = 180⁰

=>      x = 180⁰ - 152⁰ = 28⁰

So, the required angle is 28⁰ ................(Ans.)

(iii) As the sum of the angles at a point = 360⁰

As per the condition,

        x + 80⁰ + 58⁰ + 92⁰ = 360⁰

=>     x + 230⁰ = 360⁰

=>         x = 360⁰ - 230⁰ = 130⁰

So, the required angle is 130⁰ .....................(Ans.)

Example.2) Calculate the value of x in each of the following diagram -

Ans.) (i) As the sum of the angles at a point is 360⁰

As per condition -

       90⁰ + x + 25⁰ + 85⁰ + 3x = 360⁰

=>    200⁰ + 4x = 360⁰

=>         4x = 360⁰ - 200⁰ = 160⁰

=>         x = 160⁰/4 = 40⁰

So, the respective required angles are x = 40⁰, and 3x = (40⁰ X 3) = 120⁰ ...................(Ans.)

(ii) As the sum of the angles at a point on one side of a straight line is 180⁰.

As per the condition -

       (x + 15⁰) + 60⁰ + 2x = 180⁰

=>    x + 15⁰ + 60⁰ + 2x = 180⁰

=>        3x + 75⁰ = 180⁰

=>        3x = 180⁰ - 75⁰ = 105⁰

=>         x = 105⁰/3 = 35⁰ 

So, the respective required angles are (x + 15⁰) = (35⁰ + 15⁰) = 50⁰, and 2x = (2 X 35⁰) = 70⁰..........................(Ans.)

Example.3) The adjoining diagram shows two intersecting lines, calculate the value a, b, and c

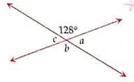
Ans.)  As per the given diagram -

         b = 128⁰       (vertically opposite angles)

so,  a + 128⁰ = 180⁰  (angles on a straight line)

=>     a = 180⁰ - 128⁰ = 52⁰

so, c = a = 52⁰  (vertically opposite angles)         

So, the values are a = 52⁰, b = 128⁰, and c = 52⁰.        (Ans.)         

Example.4) Two complementary angle are in the ratio of 2:3, find these angles.

Ans.) Since the given angles are in the ratio 2:3, let the angles be 2x, and 3x.

As the given angles are complementary angles,

so,  2x + 3x = 90⁰

=>     5x = 90⁰

=>       x = 90⁰/5 = 18⁰

now,  2x = (2 X 18⁰) = 36⁰

and,   3x = (3 X 18⁰) = 54⁰

So, the required angles are 36⁰ and 54⁰.

Example.5) If two angles are supplementary angles, and one angle is 30⁰ less than twice the other, find the angles.

Ans.) Let, if one angle be x⁰, then another be (2x - 30)⁰.

As per the given condition, angles are supplementary angle.

So,     x⁰ + (2x - 30)⁰ = 180⁰

 =>     x⁰ + 2x⁰ - 30⁰ = 180⁰

 =>       3x⁰ = 180⁰ + 30⁰

 =>       3x⁰ = 210⁰

 =>        x⁰ = 210⁰/3 = 70⁰

If x⁰ = 70⁰, then (2x - 30)⁰ = {(2 X 70⁰) - 30⁰} = (140⁰ - 30⁰) = 110⁰

So, the required angles are 70⁰ and 110⁰.        (Ans.)