CLASS-6
SUPPLEMENTARY ANGLE
SUPPLEMENTARY ANGLE -
Supplementary angles are a pair of angles whose measures add up to 180∘. In other words, if you have two angles A and B such that A + B = 180∘, then A and B are supplementary angles.
Mathematically, if A and B are supplementary angles, we write:
A + B = 180∘
Here are some key points about supplementary angles:
- Sum of Measures:- The sum of the measures of supplementary angles is always 180∘.
- Examples:- 60∘ and 120∘ are supplementary angles because 60∘ + 120∘ = 180∘. 90∘ and 90∘ are also supplementary because 90∘ + 90∘ = 180∘.
- Straight Line:- Supplementary angles are often associated with a straight line. If two angles form a straight line, they are supplementary.
- Symbolically:- If A and B are supplementary angles, we can express this relationship as A ∥ B, where ∥ represents parallel lines.
- Supplementary Pairs:- Supplementary angles form pairs, and each angle in the pair supplements the other.
- Complementary vs. Supplementary:- The main difference between complementary and supplementary angles is the sum they make. Complementary angles add up to 90∘, while supplementary angles add up to 180∘.
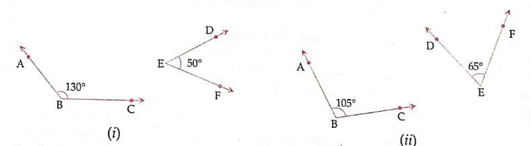
In figure (i),
∠ABC + ∠DEF = 130° + 50° = 180°
So, sum of their measures is 180°, therefore ∠ABC & ∠DEF are supplementary.
In figure (ii),
∠ABC + ∠DEF = 105° + 65° = 170°
So, sum of their measures is not 180°, therefore ∠ABC & ∠DEF are not supplementary.
Example.1) Find the Supplement of the angle 1/3 of 210°.
Ans.)
Step 1:- Convert 1/3 of 210° That is, 1/3 x 210° = 70°
Step 2:- Supplement of 70° = 180° – 70° = 110° Therefore, Supplement of the angle 1/3 of 210° is 110°. (Ans.)
Example.2) The measures of two angles are (x + 25)° and (3x + 15)°. Find the value of x if angles are supplementary angles.
Ans.) We know that, Sum of Supplementary angles = 180 degrees So,
(x + 25)° + (3x + 15)° = 180°
4x + 40° = 180°
4x = 140°
x = 35°
The value of x is 35 degrees. (Ans.)
Understanding supplementary angles is important in geometry, especially when dealing with parallel lines and transversals, as well as when studying angles formed by intersecting lines and shapes.