CLASS-6
VERTICALLY OPPOSITE ANGLE
VERTICALLY OPPOSITE ANGLE -
When two straight lines intersect each other, they form four angles at their point of intersection say a, b, c, and d.
Angles a & c are called vertically opposite angles to each other and so are angles b & d.
They are called vertically opposite angles because they have the same vertex and are opposite to each other.
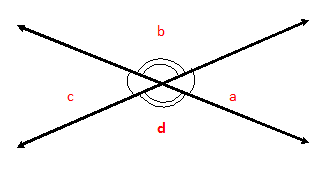
Properties Of Vertically Opposite Angles -
(i) The adjacent angles are supplementary angles.
As angles a & b are on a straight line,
So, ∠a + ∠b = 180⁰
Hence, angles a & b are supplementary angles.
Similarly, angles b & c, angles c & d, angles a & d, are supplementary angles.
(ii) Vertically opposite angles are equal.
As a & b are on a straight line So, ∠a + ∠b = 180⁰ ...............(1)
Also, as angles b & c are on a straight line.
So, ∠b + ∠c = 180⁰ ...............(2)
From (1) & (2), we get -
∠a + ∠b = ∠b + ∠c
=> ∠a = ∠c
In the same way, we can show that ∠b = ∠d