CLASS-6
SECENT OF A CIRCLE

SECENT OF A CIRCLE -

A secant of a circle is a line that intersects the circle at two distinct points. In other words, it's a straight line that "cuts across" the circle. Unlike a chord, a secant doesn't necessarily have its endpoints on the circle itself; it can extend beyond the circle.

Here are some key points about secants of circles:-

1) Intersecting Points:-  A secant intersects the circle at two points. These points can be inside, on, or outside the circle, depending on the position of the secant.

2) Secant-Secant Theorem:-  If two secants intersect outside a circle, then the measure of the angle formed by the two secants is equal to half the difference of the measures of the intercepted arcs.

3) Secant-Tangent Theorem:-  If a secant and a tangent intersect at a point outside the circle, then the measure of the angle formed is equal to half the difference of the measures of the intercepted arcs.

4) Secant-Chord Theorem:-  If a secant and a chord intersect in the exterior of a circle, then the product of the lengths of the whole secant segment and its external segment is equal to the product of the lengths of the entire chord and its external segment.

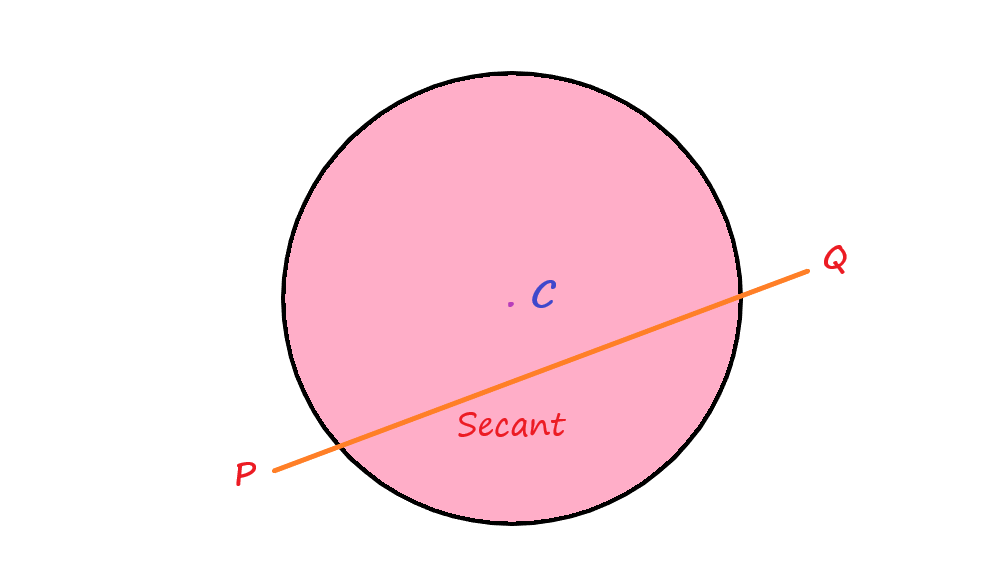
A line which meets a circle in two points is called a secant of the circle. I the abive figure, line PQ is a secant of the circle with centre C.

A line can meet a circle atmost in two points.

Secants are fundamental in circle geometry and are used in various theorems and problem-solving scenarios. They help determine relationships between angles, lengths of segments, and measures of arcs within circles.