CLASS-6
CONSTRUCTION OF 45 DEGREE ANGLE 

CONSTRUCTION OF 45 DEGREE (45⁰) ANGLE -

To construct a 45-degree angle using a compass and straightedge, you can follow these steps:

  1. Draw a base line:- Start by drawing a straight line, which will be the base for your angle.
  2. Place the compass at one endpoint:- Place the compass point (the sharp end) on one endpoint of the base line.
  3. Adjust the compass width:- Open the compass to a width greater than half the length of the base line. This will ensure that the arc you draw will intersect the base line on both sides.
  4. Draw an arc:- With the compass set, draw an arc that intersects the base line.
  5. Place the compass at the other endpoint:- Move the compass point to the other endpoint of the base line.
  6. Draw another arc:- Without changing the compass width, draw another arc from the second endpoint. This arc should intersect the first arc you drew.
  7. Draw the angle bisector:- Mark the intersection point of the two arcs. Place the compass point on this intersection point and draw an arc that intersects both arcs.
  8. Draw the angle bisector line:- Draw a straight line from one endpoint through the intersection point to the other side of the base line.
  9. Measure the angle:- The angle formed by the intersection of the base line and the bisector is a 45-degree angle.

This construction uses the property that an angle bisector of a 90-degree angle creates two congruent 45-degree angles. Make sure to use a ruler to draw straight lines and a compass to create accurate arcs.


Another Way Of Draw 45⁰ Angle :-

Step.1) Take a point O and draw any line OA to X axis and OB to Y axis. 

Step.2) With zero (0) as centre and suitable radius, draw an arc to cut the line at the points A & B.

Geometry

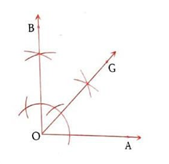
Step.3) Construct AOB, and 

                             ∠AOB = 90⁰

Step.4) Bisect ∠AOB. Let ray OG be the bisector of ∠AOB,

                       then ∠AOG = 45⁰