CLASS-6
FUNDAMENTAL CONCEPT OF GEOMETRY
FUNDAMENTAL CONCEPT OF GEOMETRY -
Geometry is a branch of mathematics that deals with the study of shapes, sizes, properties of space, and the relationships between various objects in space. It's a fundamental concept in mathematics and has numerous real-world applications. Here are some fundamental concepts in geometry:-
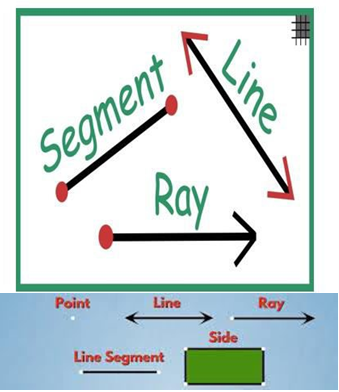
Points, Lines, and Planes: These are the basic building blocks of geometry.
(i) Points:-
- A point is a location in space, represented by a dot and having no dimension.
- A point is a mark of position. It has neither length nor width nor. thickness and occupies no space. A point determines a location. It is usually denoted by a capital letter

(ii) Line:-
A line has only length. It has neither width nor thickness. It is a one-dimensional figure having the following features:
1. It is straight (has no bends),
2. Has no thickness
3. And it extends in both directions without any end (could be extended infinitely from both ends).
4. A line is a straight path of points that extends infinitely in both directions.

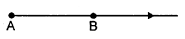
(iii) Ray:-
It is a line (i.e. a straight line) that starts from a given fixed point and moves in the same direction.
A ray is a portion or part of a line which begins at a point (which cannot be extended any further) and goes off or extends in a particular direction to infinity.
The sun rays are a popular example as they initiate from a source point called sun and the rays extend to a particular direction till infinity.
(iv) Line Segment:-
A line segment is a part of a straight line. A line segment is a part of a line and also of a ray. A line segment refers to the shortest or the least distance between two points. The line segment joining two points say A and B are denoted by AB (bar).

(v) Surface:-
A surface has length and width, but no thickness.
(vi) Plane:-
It is a flat surface. A plane has length and width, but no thickness. A plane is a flat surface that extends infinitely in all directions.
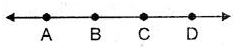
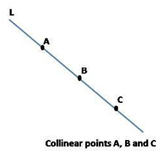
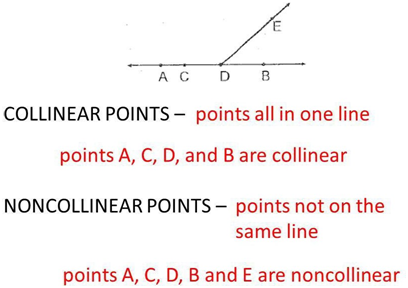
(vii) Collinearity of Points:-
If three of more points lie on the same straight line, then the points are called collinear points.
(viii) Angles:-
An angle is formed when two rays share a common endpoint. The degree of rotation between the rays measures the angle.
(ix) Polygons:-
These are closed geometric shapes with straight sides. Common polygons include triangles, quadrilaterals, pentagons, and hexagons.
(x) Circles:-
A circle is a set of points in a plane that are equidistant from a central point. Circles have a constant radius and are defined by their diameter, circumference, and area.
(xi) Congruence and Similarity:-
Congruent shapes have the same shape and size, while similar shapes have the same shape but different sizes. These concepts are essential for comparing and analyzing shapes.
(xii) Triangles:-
Triangles are three-sided polygons. They have various classifications based on their angles (acute, obtuse, right) and side lengths (equilateral, isosceles, scalene).
(xiii) Quadrilaterals:-
Four-sided polygons, including rectangles, squares, parallelograms, trapezoids, and rhombi.
(xiv) Circles and Circular Geometry:-
Concepts related to circles include the circumference, diameter, radius, central angles, and arc length.
(xv) Area and Perimeter:-
Area measures the amount of space inside a shape, while perimeter measures the total length of its boundary.
(xvi) Coordinate Geometry:-
The use of coordinates to represent points and equations to describe lines and curves.
(xvii) Transformations:-
These include translations, rotations, reflections, and dilations, which change the position, orientation, or size of geometric figures.
(xviii) Symmetry:-
The property of figures that remain unchanged when they are flipped, rotated, or reflected.
(xix) Trigonometry:-
The study of relationships between the angles and sides of triangles. It has applications in measuring distances, heights, and angles in various fields.
(xx) Solid Geometry:-
The study of three-dimensional shapes, including prisms, pyramids, cylinders, cones, and spheres.
(xxi) Geometric Proofs:-
Using logical reasoning to demonstrate the validity of geometric statements and theorems.