CLASS-6
GEOMETRY - PARALLEL LINES
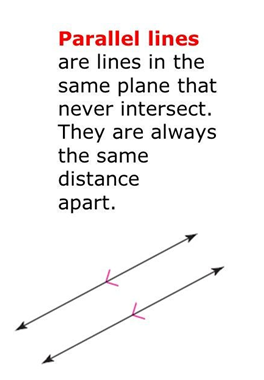
PARALLEL LINES -
Parallel lines are two or more straight lines that extend indefinitely in both directions and maintain a constant distance from each other. This means that they will never intersect, regardless of how far they are extended. In geometry, parallel lines have the same slope, and they can be found in various contexts, such as in the study of angles, triangles, and polygons.
The symbol often used to denote parallel lines is "||." For example, if line AB is parallel to line CD, it is written as AB || CD.

Key properties and concepts related to parallel lines include:-
- Transversals:- When a transversal (a line that intersects two or more other lines) crosses a pair of parallel lines, it creates corresponding angles, alternate interior angles, alternate exterior angles, and consecutive interior angles.
- Corresponding Angles:- These are angles that occupy the same relative position at each intersection where a straight line crosses two others. Corresponding angles are congruent if the lines are parallel.
- Alternate Interior Angles:- These are angles formed between a pair of parallel lines and on opposite sides of the transversal. Alternate interior angles are congruent.
- Alternate Exterior Angles:- These are angles formed between a pair of parallel lines and on opposite sides of the transversal but outside the two parallel lines. Alternate exterior angles are congruent.
- Consecutive Interior Angles:- These are angles formed between a pair of parallel lines and on the same side of the transversal. Consecutive interior angles are supplementary, meaning their sum is 180 degrees.
Understanding the properties of parallel lines and their relationships with angles is fundamental in geometry and has applications in various fields, including architecture, engineering, and physics.