CLASS-6
VERTICALLY OPPOSITE ANGLE
VERTICALLY OPPOSITE ANGLE -
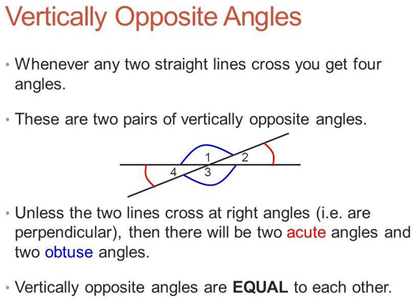
Vertically opposite angles, also known as vertical angles, are a special type of angle pair formed by the intersection of two lines. When two lines intersect, they create four angles. Vertically opposite angles are the pairs of angles opposite each other, and they share the following key properties:-
(1) Definition:-
- Vertically opposite angles are formed by the intersection of two lines. They are opposite each other at the point where the lines intersect.
(2) Location:-
- These angles are located across from each other, and their vertices are at the intersection point of the lines.
(3) Equal Measure:-
- Vertically opposite angles are always congruent (equal). This means that the measure of one angle is equal to the measure of its vertically opposite angle.
(4) Symbolically:-
- If ∠A and ∠C are vertically opposite angles, then ∠A ≅ ∠C.
(5) Relationship:-
- Vertically opposite angles share similar geometric characteristics, and their measures are equal.
In a diagram where two lines intersect, vertically opposite angles are identified as pairs of angles located across from each other. For example, if ∠A and ∠C are vertically opposite, their measures are equal.
Understanding the concept of vertically opposite angles is important in geometry and often used in proofs and problem-solving. It is a fundamental property that arises when lines intersect and is distinct from other angle relationships formed by parallel lines and transversals.