CLASS-6
FINDING HCF BY PRIME FACTORIZATION METHOD
FINDING HCF BY PRIME FACTORIZATION METHOD -
The prime factorization method is a technique used to find the highest common factor (HCF) or greatest common divisor (GCD) of two or more numbers. It involves expressing each number as a product of its prime factors and then determining the common prime factors along with their lowest exponents.
Here's how you can use the prime factorization method to find the HCF/GCD of two numbers:
Step.1) Prime Factorization
- Write down the prime factorization of each of the numbers you want to find the HCF/GCD for.
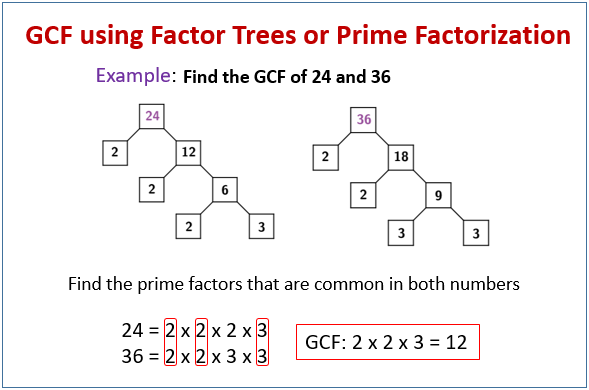
- Break down each number into a product of prime factors. For example, if you have the numbers 12 and 18:- 12 = 2^2 * 3 , 18 = 2 * 3^2
Step.2) Identify Common Prime Factors
- Compare the prime factors of the two numbers.
- Identify the common prime factors and their lowest exponents. In this example:The common prime factor is 2. The lowest exponent for the common prime factor 2 is 1.
Step.3) Calculate HCF/GCD Multiply the common prime factors with their lowest exponents to find the HCF/GCD: HCF = 2^1 = 2
So, the highest common factor (HCF) of 12 and 18 is 2.
This method can be extended to more than two numbers. Simply repeat the steps for each number and identify the common prime factors with their lowest exponents across all numbers.
Prime factorization is a powerful tool not only for finding the HCF/GCD but also for various other mathematical computations and problem-solving tasks.
The prime factorization method is a technique used to find the highest common factor (HCF) or greatest common divisor (GCD) of two or more numbers by breaking them down into their prime factors. Here's how you can use this method:
- Prime Factorization: Start by finding the prime factorization of each of the numbers. Prime factorization involves breaking down a number into a product of prime numbers that multiply together to give the original number.
- Identify Common Prime Factors: Identify the prime factors that are common to all the numbers. These common prime factors represent the factors that contribute to the HCF/GCD.
- Multiply Common Prime Factors: Multiply the common prime factors together to find the HCF/GCD.
Let's walk through an example to illustrate this process:
Example.1) Find the HCF of 48 and 60 using the prime factorization method.
- Prime Factorization:Prime factorization of 48: 48 = 48 = 2² X 2² X 3¹ Or 48 = 2^4 * 3^1, Prime factorization of 60:- 60 = 2² X 3¹ X 5¹ Or 60 = 2^2 * 3^1 * 5^1.
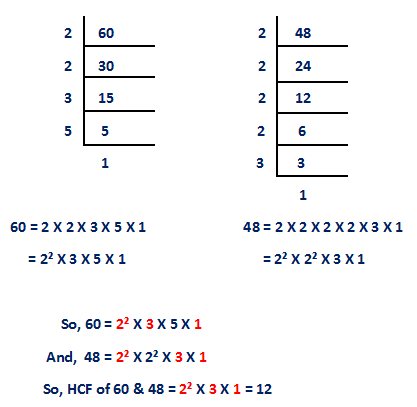
- Identify Common Prime Factors: Both 48 and 60 have a common factor of 2 raised to the power of 2 (2^2) and a common factor of 3 raised to the power of 1 (3^1).
- Multiply Common Prime Factors: Common prime factors: 2^2 * 3^1 = 4 * 3 = 12
So, the HCF of 48 and 60 is 12.
Using the prime factorization method helps you systematically find the HCF/GCD of numbers by breaking down the numbers into their fundamental prime factors and then identifying the common factors they share. This method is particularly useful when dealing with larger numbers or when you want to understand the factors contributing to the HCF/GCD more clearly.