CLASS-6
FINDING LCM BY PRIME FACTORIZATION METHOD
FINDING LCM BY PRIME FACTORIZATION METHOD -
Finding the LCM of two numbers using the prime factorization method. Let's use the numbers 24 and 36 as an example.
Example.1) Find the LCM of 24 and 36 using Prime Factorization
Step 1:- Prime factorization of 24
- 24 = 2^3 * 3^1
Step 2:- Prime factorization of 36
- 36 = 2^2 * 3^2
Step 3:- Identify distinct prime factors and their highest powers
- The distinct prime factors are 2 and 3.
- The highest power of 2 is 3 (from 2^3 in 24).
- The highest power of 3 is 2 (from 3^2 in 36).
Step 4:- Multiply the highest powers of the prime factors
- LCM = 2^3 * 3^2 = 8 * 9 = 72
So, the LCM of 24 and 36 is 72. (Ans.)
In this example, we found the prime factorization of both numbers, identified the distinct prime factors and their highest powers, and then multiplied these highest powers to obtain the LCM. You can follow similar steps to find the LCM of any other pair of numbers using the prime factorization method.
Example.2) Find the LCM of 15 and 20
- Prime factorization of 15:
15 = 3^1 * 5^1 - Prime factorization of 20:
20 = 2^2 * 5^1 - Identify the distinct prime factors and their highest powers:2^2 (from 20)3^1 (from 15)5^1 (from both 15 and 20)
- Multiply the highest powers of the prime factors: LCM = 2^2 * 3^1 * 5^1 = 4 * 3 * 5 = 60
So, the LCM of 15 and 20 is 60. (Ans.)
Remember, the prime factorization method ensures that you're finding the smallest common multiple of the given numbers by considering the highest powers of all the prime factors involved. This method is reliable and systematic for finding the LCM of any set of numbers.
Example.3) Find LCM of 24 & 36
Ans.)
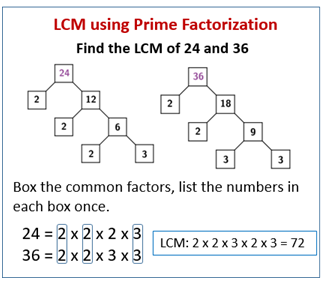
From above picture we can find -
Prime Factorization of 24 = 2 X 2 X 2 X 3
Prime Factorization of 36 = 2 X 2 X 3 X 3
As we know that, LCM = Common Factor X Uncommon Factor
So, LCM of 24 & 36 = 2 X 2 X 3 X 2 X 3 = 72 (Ans.)
Example.4) Find LCM of 264 & 624.
Ans.)
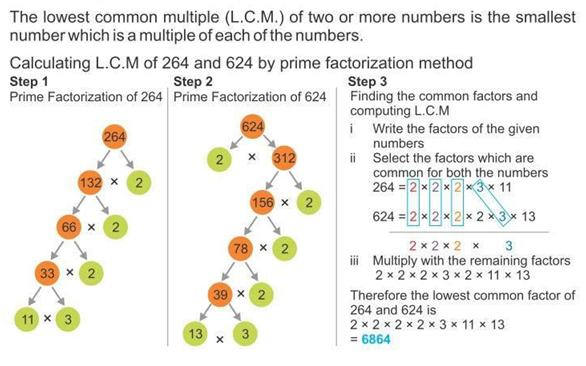
From above picture we can find -
Prime Factorization of 264 = 2 X 2 X 2 X 3 X 11
Prime Factorization of 624 = 2 X 2 X 2 X 2 X 3 X 13
As we know that, LCM = Common Factor X Uncommon Factor
So, LCM of 264 & 624 = 2 X 2 X 2 X 3 X 2 X 11 X 13 = 6864 (Ans.)