CLASS-6
LEAST COMMON MULTIPLE (LCM)
LEAST COMMON MULTIPLE (L.C.M)
The L.C.M of two or more natural numbers is the smallest of the common multiple of the given numbers. For an example, if we consider 3, 5 & 15 then the common multiples are –
Multiples of 3 are – 3, 6, 9, 12, 15, 18, 21, 24, 27,………………….....
Multiples of 5 are – 5, 10, 15, 20, 25, 30, 35, 40, 45,……………...…
Multiples of 15 are – 15, 30, 45, 60, 75, 90, 105,…………………
From the above factors, we can find that, the Least Common Factors (L.C.M) of the three given number 3, 5, & 15 is 15. (Ans.)
METHOD OF FINDING THE L.C.M THROUGH PRIME FACTORIZATION PROCESS -
1) Find the L.C.M of 32 & 48

So, 32 = 2 x 2 x 2 x 2 x 2 x 1
48 = 2 x 2 x 2 x 2 x 3 x 1
From the above factorization 2 appears in 32 five times and in 48, 2 appears four times. And also 3 appears once in a factorization of 48
Thus, 2appears maximum five times and 3 appears maximum one times
So, the Least common factor (L.C.M) of the given numbers 32 & 48 are = 2 x 2 x 2 x 2 x 2 x 3 = 96. (Ans.)
2) Find the L.C.M of 32, 48, 72
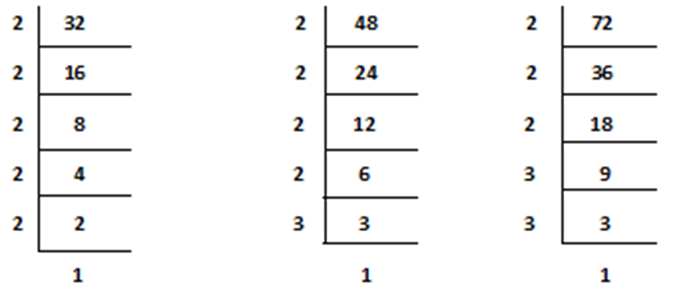
So, 32 = 2 x 2 x 2 x 2 x 2 x 1
48 = 2 x 2 x 2 x 2 x 3 x 1
72 = 2 x 2 x 2 x 3 x 3 x 1
From the above factorization 2 appears in 32 five times, 2 appears in 48 four times and 2 appears three times in 72. And also
3 appears one time in a factorization of 48 and 3 appears two times in 72.
Thus, 2 appears maximum five times and 3 appears maximum two times
So, the Least common factor (L.C.M) of the given numbers 32, 48 and 72 are = 2 x 2 x 2 x 2 x 2 x 3 x 3 = 288 (Ans.)
FIND LEAST COMMON FACTORS (L.C.M) THROUGH COMMON DIVISION METHOD -
1) Find the L.C.M of 18, 24, 27,36 & 72

Step.1) Arrange the given numbers in a row in any order you wish
Step.2) Select or take any number as a Divisor which divides exactly minimum of two given numbers in a row and carries forward the rest of the non-divisible numbers to the next step.
Step.3) Repeat the above process till no two of the given numbers are Divisible by same number other than 1.
Step.4) The product of the divisors and the undivided numbers is the required L.C.M of the given numbers.