CLASS-6
INTRODUCTION OF CUBOID
DEFINITION OF CUBOIDS -
A cuboid, also known as a rectangular prism, is a three-dimensional geometric shape with six rectangular faces, 12 straight edges, and eight vertices (corners). In a cuboid, the opposite faces are parallel and equal in pairs. Each face forms a right angle with the adjacent faces. The cuboid is a polyhedron, a type of three-dimensional solid with flat faces.
Recognition of a Cuboid:-
To recognize a cuboid, you can look for several key characteristics:
- Rectangular Faces:- A cuboid has six faces, and each of these faces is a rectangle. These rectangular faces are organized into three pairs of opposite, parallel rectangles.
- Right Angles:- All the angles between adjacent faces (edges) of a cuboid are right angles (90 degrees). This is a distinguishing feature of a cuboid.
- Equal Opposite Faces:- In each pair of opposite faces, the rectangles have the same dimensions (length and width), making them congruent to each other.
- Equal Edges in Pairs:- The edges are organized into three pairs of equal length. In each pair, the edges are of the same length.
- Equal Diagonals in Pairs:- Each pair of opposite faces of a cuboid has two diagonals, which are equal in length within each pair.
- Vertices:- A cuboid has eight vertices (corners), where three edges meet.
Example:-
Let's consider an example of recognizing a cuboid in a real-world context:
Scenario: You are given a rectangular wooden box.
Recognition Steps:-
- Observe the faces:- Count the number of faces. A cuboid has six faces.
- Check for right angles:- Examine the corners where the faces meet. Verify that the angles between the faces are right angles (90 degrees).
- Look for opposite faces:- Identify two pairs of opposite faces. These faces should have the same dimensions and be parallel to each other.
- Measure the edges:- Measure the length of the edges of the wooden box. In a cuboid, three pairs of edges should have equal lengths.
- Examine the diagonals:- Calculate the length of the diagonals within each pair of opposite faces. These diagonals should be equal in length.
- Count the vertices:- Count the number of vertices. A cuboid should have eight vertices where three edges meet.
- Confirm congruency:- Ensure that the opposite faces are congruent (equal in size and shape).
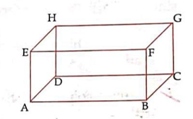
The adjoining figure shows Cuboid.
In every day's life we come across so many object that appear to be of cuboid shape. A brick, a chalk box, a match box, a die, etc. all are example of cuboid shape. A cuboid has 6 rectangular faces. The top and bottom face form one pair (congruent) of opposite faces. The front and back faces form another pair of (congruent) opposite faces, and the two side faces form third pair of (congruent) opposite faces. Any two faces other than the opposite, called the adjacent faces meet in the line segment, which is called an edge of the cuboid. The points of the intersections of three faces is called a vertex (corner) of the cuboid.
Cuboid has twelve (12) edges and eight (8) vertices.
In the above cuboid, EFGH is the top face, ABCD is the bottom face, EABF is the front face, HDCG is the back face, EADH & FBCG are the two side faces. The edges of the cuboid are EF, HG, AB, DC, AD, BC, EH, FG, EA, HD, FB, & GC.
The vertices (corners) of the cuboid are A, B, C, D, E, F, G, & H.
Since the opposite edges of a cuboid are equal, so we see that -
EF = HG = AB = DC,
EH = AD = FG = BC,
EA = HD = FB = GC,
Thus, the cuboid has only three distinct length, which are called length, height, and width of a cuboid.
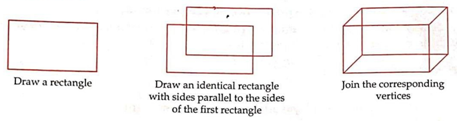
To draw a cuboid:-