CLASS-6
SURFACE AREA OF CUBOID

SURFACE AREA OF CUBOID -

Surface are of a cuboid is the sum of the areas of all its six rectangular faces.

The adjoining diagram shows a cuboid with, length = l units

breadth = b units,

and, height = h units,

The six faces of the cuboid are shown below -

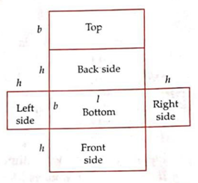
1) There are two faces (top & bottom) each with area = l X b sq.units

2) There are two faces (front & back) each with area = l X h sq.units

3) There are two faces (right & left) each with area = b X h sq.units

The surface area of the cuboid

= sum of areas of all six faces

= 2 (lb + lh + bh) sq.units

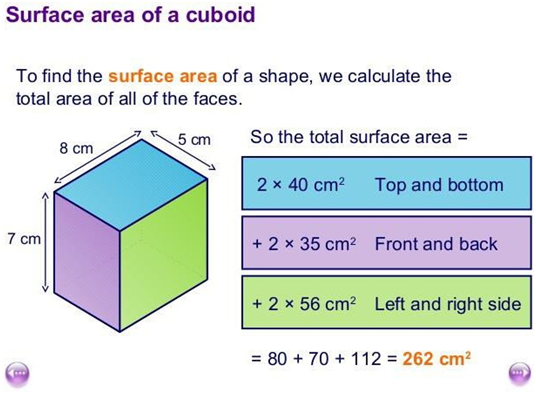
Example.1) Let's say you have a rectangular box (cuboid) with the following dimensions:

Ans.)

To find the surface area of this cuboid, you would use the formula:

Surface Area = 2(lw + lh + wh)

Surface Area = 2 {(8 cm X 5 cm) + (8 cm X 3 cm) + (5 cm X 3 cm)}

Surface Area = 2(40 cm² + 24 cm² + 15 cm²)

Surface Area = 2 (79 cm²)

Surface Area = 158 cm²

So, the surface area of this cuboid is 158 square centimeters. (Ans.)

Example.2) Suppose you have a rectangular storage container with the following measurements:

Ans.)

To calculate the surface area, use the formula:

Surface Area = 2(lw + lh + wh)

Surface Area = 2 {(12 in X 6 in) + (12 in X 4 in) + (6 in X 4 in)}

Surface Area = 2 (72 in² + 48 in² + 24 in²)

Surface Area = 2 (144 in²)

Surface Area = 288 in²

The surface area of this rectangular storage container is 288 square inches. (Ans.)

CLASS-6SURFACE AREA OF CUBOID