CLASS-7
ALGEBRAIC-INTRODUCTION OF SIMPLIFICATION

Introduction of Simplification

In Arithmetic, there can be fractions in algebra too. An algebraic fraction can have a monomial or polynomial in the numerator or denominator or both.

Examples – 1)  X/9  and  (2X²+ X)/6 are algebraic fractions with integral denominators

             2)  7/ X⁵ and 15/ ( X⁴ + 3X² ) are algebraic fraction with integral numerators

             3)  X / ( X⁴ + 8 ) has a monomial in the numerator and a polynomial in the denominator

             4)  ( 4X⁵ + 11 ) / ( 3X⁷ - 5 ) has a polynomial in the both numerator and denominator .

Fraction is always expressed in the simplest form, by canceling out the common factors in the numerator and denominator.

As example, we can see that, in a fraction if the numerator is -

 (12a⁵b²c⁴ + 18a⁴bᶟc⁵) and the denominator is ( 6a⁷b⁶c⁴ - 12a⁶b⁴c⁵ ) ,

                                ( 12a⁵b²c⁴ + 18a⁴bᶟc⁵ )    

Then the fraction is =>  --------------------------

                                 ( 6a⁷b⁶c⁴ - 12a⁶b⁴c⁵ )

In first step, we have to find out the common factor from both numerator and denominator,

So, in numerator the common factor is 6a⁴b²c⁴ and the numerator should be looked like this  6a⁴b²c⁴ ( 2a + 3bc ) and in case of denominator common factor is 6a⁶b⁴c⁴ and denominator should be look like this 6a⁶b⁴c⁴ ( ab² - 2c ), now the equation would be look like this –

     12a⁵b²c⁴ + 18a⁴bᶟc⁵               6 a⁴ b² c⁴ ( 2a + 3bc ) 

 ----------------------   =   -------------------------

      6a⁷b⁶c⁴ - 12a⁶b⁴c⁵                6 a⁶ b⁴ c⁴ ( ab²- 2c )  

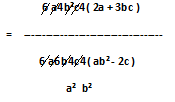
            ( 2a + 3bc )

=   ---------------------------

         a²b² ( ab² - 2c )

a) The rules for the addition, subtraction, multiplication, and division of algebraic fractions are the same as those for fractions in arithmetic. Here we will consider only algebraic fractions with integral denominators.

b) Algebraic fractions are expressed in the simplest form by canceling the common factors in the numerator and the denominator  

         x                  y                      

c)  ----------  X  ----------   

         A                  B 

               xy

=  ------------

               AB

         x                y                

d)  ---------  ÷  ---------       

         A                B 

          x                 B

=  ---------  X  --------- 

              A                 y

          Bx

=   -----------

          Ay

 

          x                   y                            

d)   ----------  +   -----------      

          A                   B        

  Let assume LCM of  A & B is  Z, then

               x X ( Z ÷ A ) + y X ( Z ÷ B )

   =    ----------------------------------   

                            Z

 

 

 

              x                  y                            

e)      ----------  -   -----------      

              A                  B        

  Let assume LCM of  A & B is  Z, then

            x  X ( Z ÷ A )  -  y X ( Z ÷ B )

   =   ------------------------------   

                           Z