CLASS-7
ALGEBRAIC PROBLEM SOLUTION
Problem & Solution
Multiply every equations which are given below –
1) (X + 4b) (X – 3a) = ?
Ans.) (X + 4b) (X – 3a)
= X. (X – 3a) + 4b. (X – 3a)
= X² - 3aX + 4bX – 12ab (Ans.)
2) ( X²- 4 ) ( X²- 5 ) + X ( X + 8 ) = ?
Ans.) ( X² - 4 ) ( X² - 5 ) + X ( X + 8 )
= X². ( X² - 5 ) – 4 . ( X² - 5 ) + X . X + 8X
= X². X² - 5 X² - 4 X² + 20 + X¹⁺¹ + 8X
= X²⁺² - 9X² + 20 + X² + 8X
= X⁴ - ( 9 – 1) X² + 8X + 20
= X⁴ - 8X² + 8X + 20 (Ans.)
3) ( X + 5 ) ( X – 6 ) ( X – 4 ) + Xᶟ - 4 X² + 3 X – 20 = ?
Ans.) ( X + 5 ) ( X – 6 ) ( X – 4 ) + Xᶟ - 4 X² + 3 X – 20
= { X . ( X – 6 ) + 5 . ( X – 6 ) } ( X – 4 ) + Xᶟ - 4 X² + 3 X – 20
= {( X² - 6X + 5X – 30 ) ( X – 4 )} + Xᶟ - 4 X² + 3 X – 20
= { X² - ( 6 – 5 ) X – 30 } ( X – 4 ) + Xᶟ - 4 X² + 3 X – 20
= ( X² - X – 30 ) ( X – 4 ) + Xᶟ - 4 X² + 3 X – 20
= X² ( X – 4 ) – X ( X – 4 ) – 30 ( X – 4 ) + Xᶟ - 4 X² + 3 X – 20
= X²⁺¹ - 4X² - X¹⁺¹ + 4X – 30X + 120 + Xᶟ - 4 X² + 3 X – 20
= Xᶟ - 4X² - X² - 26X + 120 + Xᶟ - 4X² + 3 X – 20
= ( 1 + 1 ) Xᶟ - ( 4 + 1 + 4 ) X² - ( 26 – 3 ) X + 120 – 20
= 2 Xᶟ - 9 X² - 23 X + 120 – 20
= 2Xᶟ - 9X² - 23X + 100 (Ans.)
Simplify the following using a special product
1) ( 2X – 5a )² = ?
Ans.) ( 2X – 5a )²
= ( 2X – 5a ) ( 2X – 5a )
= 2X ( 2X – 5a ) - 5a ( 2X – 5a )
= 2.2 X¹⁺¹- 2X.5a - 5a.2X + 5a.5a
= 4X²- 10aX - 10aX + 25a²
= 4X²- 20aX + 25a²
We can get the same result via applying formula –
( a – b )² = a² - 2ab + b²
So, as per the given condition with applying formula
( 2X – 5a )²
= (2X)²- 2 (2X. 5a) + 25a²
= 4X²- 20aX + 25a² (Ans.)
2) ( 3x + 5b )² = ?
Ans.) ( 3x + 5b )²
= ( 3x + 5b ) ( 3x + 5b )
= 3x. ( 3x + 5b ) + 5b ( 3x + 5b )
= 3.3 x¹⁺¹ + 3x.5b + 5b.3x + 5.5 b¹⁺¹
= 9x² + 15xb + 15xb + 25b²
= 9x² + 30xb + 25b² (Ans.)
We can get the same result via applying formula –
( a + b )² = a² + 2ab + b²
So, as per the given condition with applying formula
( 3x + 5b )²
= (3x)² + 2 (3x.5b) + (5b)²
= 9x² + 30xb + 25b² (Ans.)
3) ( 3X – 1 / 2X)² = ?
1
( 3X - --------- ) ²
2X
1 1
= ( 3X - --------- ) . ( 3X - -------- )
2X 2X
1 1 1
= 3X . ( 3X - ------- ) - -------- . ( 3X - ------- )
2X 2X 2X
3X 3X 1
= 3X . 3X - -------- - --------- + -----------
2X 2X 2X . 2X
3 3 1
= 9X² - ------- - ------- + -------
2 2 4X²
1
= 9X² + -------- - 3 (Ans.)
4X²
We can get the same result via applying formula –
( a – b )² = a² - 2ab + b²
So, as per the given condition with applying formula
1
( 3X - ------ ) ²
2X
1 1²
= ( 3X )² - 2 . 3X . ------- + ( -------- )
2X 2X²
1
= 9X² - 3 + --------
4X²
1= 9X² + ------- - 3 (Ans.)
4X²
Find the square of each of the following binomial –
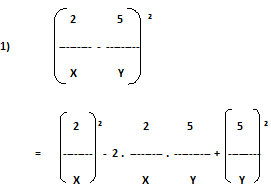
2² 0 25
= --------- - --------- + ---------
X² XY Y²
Express each of the following equations as the square of a binomial
1) a² - 16ab + 64b²
Ans.) a² - 16ab + 64b²
= a² - 2a . 8b + (8b)²
= ( a – 8b )² (Ans.)
2) 25a² + 40ab + 16b²
Ans.) 25a² + 40ab + 16b²
= (5a)² + 2. 5a . 4b + (4b)²
= ( 5a + 4b )² (Ans.)
Find the value of the following using special products –
1) 199² = ?
Ans.) 199² = ( 200 – 1)²
= 200² - 2 . 200 . 1 + 1²
= 40000 – 400 + 1
= 39600 + 1
= 39601
2) 310² = ?
310² = ( 300 + 10 )²
= 300² + 2. 300 . 10 + 10²
= 90000 + 6000 + 100
= 96100 (Ans.)
3) 4.5 X 5.5 = ?
4.5 X 5.5 = ( 5.00 – 0.50 ) X ( 5.00 + 0.50 )
= ( 5.00 )² - ( 0.50 )²
= 25 -0.25
= 24.75 (Ans.)
4) 3.6 X 4.4 = ?
3.6 X 4.4 = ( 4.00 – 0.40 ) X ( 4.00 + 0.40 )
= ( 4.00 )² - ( 0.40 )²
= 16 - 0.16
= 15.84 (Ans.)
5) 10.2 X 9.8 = ?
10.2 X 9.8 = ( 10.00 + 0.20 ) X ( 10.00 – 0.20 )
= ( 10.00 )² - ( 0.20 )²
= 100 – 0.04
= 99.96 (Ans.)