CLASS-7
INTRODUCTION OF FRACTION
INTRODUCTION OF FRACTION -
A fraction is a way of representing a part of a whole. It is a fundamental concept in mathematics that allows us to express quantities that are not whole numbers. Fractions are used to describe portions of objects, amounts, or numbers. Structure of a Fraction:
A fraction consists of two parts:-
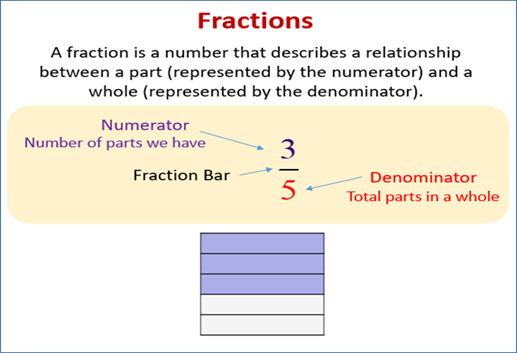
- Numerator:- The top part of the fraction, representing how many parts we have.
- Denominator:- The bottom part of the fraction, representing the total number of equal parts the whole is divided into.
The general form of a fraction is:-
Numerator
----------------
Denominator
Examples of Fractions:-
1
1. Simple Fraction:- -------, This means one part out of two equal
2
parts, often read as "one-half."
3
2. Proper Fraction:- -------, This means three parts out of four
4
equal parts, often read as "three-fourths." The numerator is less than the denominator.
5
3. Improper Fraction:- -------, This means five parts out of three
3
equal parts. Here, the numerator is greater than the denominator, indicating a quantity greater than one whole.
1
4. Mixed Number:- 2 ------- This is a combination of a whole
2
number and a fraction, representing a value greater than one but not a whole number.
Types of Fractions:-
- Proper Fractions:- Where the numerator is less than the denominator (e.g., 3/5)
2. Improper Fractions:- Where the numerator is greater than or equal to the denominator (e.g., 7/4).
3. Mixed Numbers:- A combination of a whole number and a proper
1
fraction (e.g., 3 ------).
4
4. Equivalent Fractions:- Different fractions that represent the same value (e.g., 1/2 is equivalent to 2/4).

Basic Operations with Fractions:-
1. Addition and Subtraction:-
Fractions must have the same denominator to be added or subtracted. For example,
1 2 (1 + 2) 3
------- + ------- = ---------- = ------- and,
4 4 4 4
1 2 (2 - 1) 1
------- - ------- = ---------- = ------
4 4 4 4
2. Multiplication:- Multiply the numerators together and the denominators together. For example,
2 3 1
------ X ------ = ------
3 4 2
3. Division:- Multiply by the reciprocal of the divisor. For example,
2 4 2 5 (2 X 5) 5
------ ÷ ------ = ------ X ------ = ----------- = ------
3 5 3 4 (3 X 4) 6
Real-Life Applications:-
- Cooking:- Recipes often require ingredients in fractional amounts, like 1/2 cup of sugar.
- Measurement:- Fractions are used to express measurements, such as 3/4 inch.
- Money:- Understanding fractions is crucial when dealing with currency, especially when splitting amounts or calculating discounts.
Summary:-
Fractions are essential for expressing parts of a whole in mathematics and everyday life. They allow us to work with quantities that are not whole numbers, enabling precise calculations and measurements. Understanding fractions is fundamental to arithmetic, algebra, and various real-world applications.