CLASS-7
ROOTS

INTRODUCTION OF ROOTS

When a number is multiplied by itself repeatedly, the number is called the root of the product. Thus 4 is a root of (4 X 4), (4 X 4 X 4), (4 X 4 X 4 X 4),……., we will consider square root and cube roots. The square root of the number is the number which when multiplied by itself is equal to the given number. The symbol for the square root is √ or ( )½ . If any product is a multiplication of the same number then the root of that product would be any one of the same number, we can also express the number as a product of powers of prime factors, taking half of each index and then finding the product of the factors will give the square root.  If a is multiplied by a and we get the product a², a X a = a² , then the root would be    √a²  =  √a X a  = a

Example -

1) If 11 is base and square of 11 is  = 11² = 121 ,

But when we try to find out the root of 121, then 121 = 11 X 11

And root would be √ 11 X 11  =  11

2) If 11 is base and square of 15 is  = 15² = 225 ,

But when we try to find out the root of 225, then 225 = 15 X 15

And root would be √ 15 X 15  =  15

The above process is about a small number till the table number 20 or 25, but what about big numbers?

So, for the big numbers, it is not easy to find the square roots of bigger numbers and in such cases, there are two way of finding root-

1) by Prime Factorization       and        2) by Division

Process of Finding Root via Prime Factorization -

1) Express the number as a product of prime factors

2) Make pairs of equal prime factors

3) Take one factor from each pair and multiply them. 

Example-

1) Find out the root of 1024 via the prime factorization method.

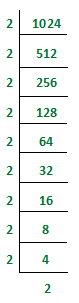
1024 =  2 X 2 X 2 X 2 X 2 X 2 X 2 X 2 X 2 X 2  [Express the number as a product of prime factors]

√1024 = √ (2 X 2 ) X √ ( 2 X 2 ) X √ ( 2 X 2 ) X √ ( 2 X 2 ) X √ ( 2 X 2 ) [Make pairs of equal prime factors]

√1024 =  2 X 2 X 2 X 2 X 2  = 32    [Take one factor from each pair and multiply them.] 

2) Find out the root of 625 via the prime factorization method.

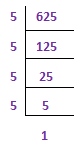
625 = 5 X 5 X 5 X 5     [Express the number as a product of prime factors]

√625 = √ (5 X 5 ) X √ ( 5 X 5 )    [Make pairs of equal prime factors]

√625 = 5 X 5  = 25     [Take one factor from each pair and multiply them.]