CLASS-7
FINDING AREA OF PATH INSIDE OR OUTSIDE OF RECTANGLE & SQUARE
FINDING AREA OF PATH INSIDE OR OUTSIDE OF RECTANGLE & SQUARE -
(a) The length and breadth of the rectangle should be given or if it is a square, then each side should be given.
(b) The width of the path should be given.
(c) If the path is made outside the given rectangle, then the length and breadth of the outer rectangle should be calculated by adding the width of the path twice to the inner length and breadth respectively to add it to either side of the inner length and breadth.
(d) If the path is made inside the given rectangle, then the length and breadth of the
inner rectangle should
be calculated by subtracting the width of the path twice
from the outer length and breadth respectively to remove it from either side of the outer length and breadth.
(e) Area of the path = area of outer rectangle-area of inner rectangle
Example.1) The rectangular frame of a picture is 24.5 cm wide and 36.6 cm high. The border is 3.4 cm wide. Calculate the perimeter of picture.
Ans.)
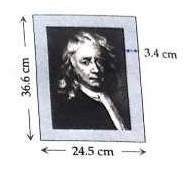
Width of picture = 24.5 cm - (3.4 + 3.4) cm
= 24.5 cm - 6.8 cm
= 17.7 cm
Height of picture = 36.6 cm - (3.4+3.4) cm
= 36.6 cm - 6.8 cm
= 29.8 cm
Now, we need to find out the perimeter of the picture, where width of the picture is 17.7 cm and height of the picture is 29.8 cm.
Formula of perimeter of the rectangle is = 2 (height + width)
So, Perimeter of picture is = 2 (29.8 + 17.7) cm
= (2 X 47.5) cm = 95 cm (Ans.)
Example.2) A rectangular lawn is 15 m long and 9 m width. It has a path of 1.5 m wide all around it. Find the area of the path.
Ans.)
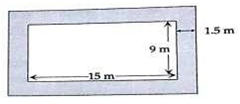
In the above figure, shaded portion is path. Length and width of the lawn is 15m & 9m respectively.
So, the area of the lawn is = length x width = 15m x 9m = 135m²
Now, as per the given condition, the length of the outer rectangle is
= 15m + (1.5m + 1.5m)
= 15m + 3m = 18m
The, width of the outer rectangle is = 9m + (1.5m + 1.5m)
= 9m + 3m = 12m
Now, if the length & width of outer rectangle are 18m & 12m respectively, then the area of the outer rectangle is -
Area of the rectangle = (length x width) = (18m x 12m) = 216m²
Now, the area of the shaded path is = (216m²- 135m²) = 81m² (Ans.)
Example.3) A path 1 meter is wide is build along the border and inside a square garden of side 30m. Find -
(i) the area of the path,
(ii) the cost of planting grass in the remaining portion of the garden at the rate of 4$ per m².
Ans.)
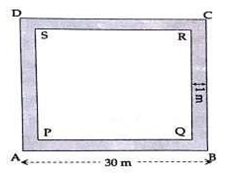
Let, ABCD be the square garden of side 30m. A path of 1m wide is built along the border inside. In the adjoining figure, the shaded portion shows the path.
Note hat, PQRS is a square of side = 30m - (1m + 1m) = 30m - 2m = 28m
Area of square ABCD = (side)²= (30)²= (30 x 30) = 900m²
Area of square PQRS = (side)²= (28)²= (28 x 28) = 784m²
So, area of path = 900m²- 784m² = 116m² .............(i) (Ans.)
Area of the remaining portion of the garden = area of square PQRS
= 784m²
As per the given condition, cost of planting grass is the remaining portion of the garden is 4$ per m²
So, the total cost of planting grass is = 784m²x 4$ = 3136$ .......(ii) (Ans.)
Example.4) Through a rectangular field of length 90m and breadth 60m, two cross roads are constructed which are parallel to the sides and cut each other at right angles through the centre of the field. If the width of each road is 3m, find -
(i) the area covered by the roads,
(ii) the cost of constructing the rods at the rate of 11$ per m².
Ans.)
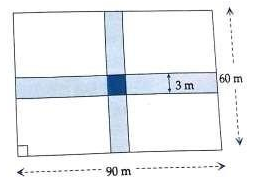
The area covered by the roads is shown shaded in the adjoining diagram. Area of the shaded portion parallel to the length = (90 x 3)m²= 270m²
Area of the shaded portion parallel to the width = (60 x 3)m²= 180m²
Area of the dark shaded portion = (3 x 3)m²= 9m²
So, the area covered by the cross roads = area of shaded portion
= (270 + 180)m²- 9m²
= 441m² ...........(i) (Ans.)
Note that we subtract the area of the dark shaded portion because it has occurred twice - firstly when considering area parallel to length and secondly when considering area parallel to the breadth.
Given, the cost of constructing the road is at the rate of 11$ per m².
The total cost of constructing the roads = (441m²x 11$) = 48510$ ...............(ii) (Ans.)