CLASS-7
PROBLEM & SOLUTION OF ALGEBRAIC EXPONENTS
PROBLEM & SOLUTIONS EXAMPLES
Express each of the following as a power of a number with a positive index –
1) 2⁴ X 64 X 2² = ?
Ans.) 2⁴ X 64 X 2²
= 2⁴ X 2⁶ X 2²
= 2⁴⁺⁶⁺²
= 2¹² (Ans.)
2) 5⁴ X 5² X 625 X 125 = ?
Ans.) 5⁴ X 5² X 625 X 125
= 5⁴ X 5² X 5⁴ X 5ᶟ
= 5⁴⁺²⁺⁴⁺ᶟ
= 5¹ᶟ (Ans.)
Express each of the following as a power of a number –
1) (3⁴)² ÷ 3⁴ = ?
Ans.) (3⁴)² ÷ 3⁴
= 3⁴ˣ² ÷ 3⁴
= 3⁸ ÷ 3⁴
= 3⁸⁻⁴
= 3⁴ (Ans.)
2) (10⁵)⁴ ÷ (10⁴)ᶟ = ?
Ans.) (10⁵)⁴ ÷ (10⁴)ᶟ
= 10⁵ˣ⁴ ÷ 10⁴ˣᶟ
= 10²⁰ ÷ 10¹²
= 10²⁰⁻¹²
= 10⁸ (Ans.)
Express each of the following as a power of a number –
1) Express (64 X 625 )⁴ as a product of the powers of 4 & 5
Ans.) (64 X 625 )⁴
= ( 4ᶟ X 5⁴ )⁴
= 4ᶟˣ⁴ X 5⁴ˣ⁴
= 4¹² X 5¹⁶ (Ans.)
Express each of the following as a power of a number with a positive index –
1) (10⁻⁵)⁶ = ?
Ans.) (10⁻⁵)⁶
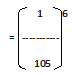
( 1 ) ⁶
= -------------
(10⁵ )⁶
1
= ------------
10⁵ˣ⁶
1
= ------------ (Ans.)
10ᶟ⁰
2) Find ( 3xᶟy² )⁵ - (4x²y⁶)² = ?
Ans.) ( 3xᶟy² )⁵ - (4x²y⁶)²
= 3⁵ xᶟˣ⁵ . y²ˣ⁵ - 4² x²ˣ² y⁶ˣ²
= 243 x⁸y⁷ - 16 x⁴y¹² (Ans.)
( 4a⁴b⁻⁶ + 3a⁻²b⁵) X 3 a⁷b⁴
3) -------------------------------
( 3a⁻⁸b⁵ - 5a⁶b⁷) X 6 a⁻⁴b⁻⁶
( 4a⁴b⁻⁶ + 3a⁻²b⁵) X 3 a⁷b⁴
Ans.) ---------------------------------
( 3a⁻⁸b⁵ - 5a⁶b⁷) X 6 a⁻⁴b⁻⁶
(4a⁴b⁻⁶ X 3 a⁷b⁴) + (3a⁻²b⁵ X 3 a⁷b⁴)
= -----------------------------------------
(3a⁻⁸b⁵ X 6 a⁻⁴b⁻⁶) – (5a⁶b⁷ X 6 a⁻⁴b⁻⁶)
{(4X3) X (a⁴ X a⁷) X (b⁻⁶X b⁴)} + { (3 X 3) X (a⁻²X a⁷) X (b⁵ X b⁴)}
= --------------------------------------------------------
{(3X6) X (a⁻⁸ X a⁻⁴) X (b⁵ X b⁻⁶)} – {(5 6) X (a⁶ Xa⁻⁴) X (b⁷X b⁻⁶)}
(12 a⁴⁺⁷ b⁻⁶⁺⁴) + (9 a⁻²⁺⁷ b⁵⁺⁴)
= ----------------------------------
(18 a⁻⁸⁻⁴ b⁵⁻⁶) – ( 30 a⁶⁻⁴b⁷⁻⁶)
12 a¹¹ b⁻² + 9 a⁵b⁹
= --------------------------- (Ans.)
18 a⁻¹² b⁻¹ - 30 a²b¹
( 4a⁴b⁻⁶ + 3a⁻²b⁵) X 3 a⁷b⁴
4) ------------------------------
6 a⁻⁴b⁶
( 4a⁴b⁻⁶ + 3a⁻²b⁵) X 3 a⁷b⁴
Ans.) -----------------------------------
6 a⁻⁴b⁶
(4a⁴b⁻⁶ X 3 a⁷b⁴) + (3a⁻²b⁵ X 3 a⁷b⁴)
= -------------------------------------
6 a⁻⁴b⁶
{(4X3) X (a⁴ X a⁷) X (b⁻⁶ X b⁴)} + {(3X3) X (a⁻²X a⁷) X (b⁵ X b⁴)}
= ------------------------------------------------------
6 a⁻⁴b⁶
12 a⁴⁺⁷ b⁻⁶⁺⁴ + 9 a⁻²⁺⁷ b⁵⁺⁴
= -------------------------------
6 a⁻⁴b⁶
12 a¹¹ b⁻² + 9 a⁵ b⁹
= ----------------------------
6 a⁻⁴b⁶
12 a¹¹ b⁻² 9 a⁵ b⁹
= --------------- + -------------
6 a⁻⁴b⁶ 6 a⁻⁴b⁶
12 9
= ------- (a¹¹ b⁻²) X (a⁻⁴b⁶)⁻¹ + -------- (a⁵ b⁹) X (a⁻⁴b⁶)⁻¹
6 6
= 2 (a¹¹ b⁻²) X (a⁻⁴ˣ⁻¹ b⁶ˣ ⁻¹) + 3/2 (a⁵ b⁹) X (a⁻⁴ˣ⁻¹ b⁶ˣ⁻¹)
= 2 (a¹¹ b⁻²) X (a⁴ b⁻⁶) + 3/2 (a⁵ b⁹) X (a⁴ b⁻⁶)
= 2 (a¹¹ X a⁴) X (b⁻² X b⁻⁶) + 3/2 (a⁵ X a⁴) X (b⁹ X b⁻⁶)
= 2 a¹¹⁺⁴ b⁻²⁻⁶ + 3/2 a⁵⁺⁴ b⁹⁻⁶
= 2 a¹⁵ b⁻⁸ + 3/2 a⁹ bᶟ (Ans.)