CLASS-7
RULES FOR FUNDAMENTAL OPERATION
RULES & EXAMPLES
Properties Of Addition – ( If, x & y are whole numbers then x + y is a whole number.)
Closure property – The sum of any two whole number should be as a whole number
Example –
1) 12 + 25 = 37, whole number
2) 48 + 120 = 168, whole number
3) 124 + 237 = 361, whole number
4) 1248 + 3045 = 4293, whole number
Commutative property – ( If, x & y are whole numbers then x + y = y + x )
Sum of two whole number remains the same irrespective of the order in which we add them and the result will be the same on each case -
Example –
1) 15 + 30 = 30 + 15
2) 100 + 221 = 221 + 100
3) 222 + 111 = 111 + 222
Associative property – [ If, x, y & z are whole numbers then ( x + y ) + z = x + ( y + z ) = x + y + z ]
If we would like to find the sum of three whole numbers then, then first we would like to add any two of the number then whatever the result will be obtained that will be added with the 3rd number.
Example –
1) 25 + 50 +75 = ( 25 + 50 ) + 75 = 25 + (50 + 75 )
=> 75 + 75 = 25 + 125 = 150 ( from both side obtained result are same )
2) 125 + 110 + 150 = ( 125 + 110 ) + 150 = 125 + ( 110 + 150 )
=> 235 + 150 = 125 + 260 = 385 ( from both side obtained result are same )
3) 200 + 1000 + 50 = ( 200 + 1000 ) + 50 = 200 + ( 1000 + 50 )
=> 1200 + 50 = 200 + 1050 = 1250 ( from both side obtained result are same )
4) 220 + 100 + 150 + 30 = ( 220 + 100 ) + ( 150 + 30 )
= ( 220 + 30 ) + ( 100 + 150 )
=> 320 + 180 = 250 + 250 = 500 ( from both side obtained result are same )
Properties of Multiplication – [ If, a & b are whole numbers then the result of a X b is also a whole number.]
The product of any two whole number would be only a whole number
Example –
1) 12 X 10 = 120
2) 1080 X 100 = 108000
3) 12 X 15 = 180
Commutative property – [ If, a & b are whole numbers then a X b = b X a ]
The product of two whole numbers remains the same irrespective of the order in which we multiply them.
Examples –
1) 12 X 15 = 15 X 12 ; 12 x 15 = 180 and 15 X 12 = 180 ; so, 12 X 15 = 15 X 12 = 180 ;
So, 12 X 15 = 15 X 12 (Proven)
2) 20 X 14 = 14 X 20 ; 20 X 14 = 280 and 14 X 20 = 280 ; So, 20 X 14 = 14 X 20 = 280 ;
So, 20 X 14 = 14 X 20 (Proven)
3) 30 X 17 = 17 X 30 ; 30 X 17 = 510 and 17 X 30 = 510 ; So, 30 X 17 = 17 X 30 = 510 ;
So, 30 X 17 = 17 X 30 (Proven)
Associative Property – [ If, a, b & c are whole numbers then a X ( b X c ) = (a X b ) X c = a X b X c ]
To find the product of three whole numbers we first multiply any of the two given number, and then the obtained product will be multiplied by 3rd number, result always would be the same and not matters which first two numbers we have multiply 1st and which 3rd number multiply with an obtained product of any of first two numbers.
Example –
1) 10 X 20 X 15 = ?
Ans.) 10 X 20 X 15 = ( 10 X 20 ) X 15 = 3000, by associative property
Changing arrangement, 10 X (20 X 15 ) = 3000 , by commutative property
( 10 X 20 ) X 15 = 10 X (20 X 15 ) = 3000
2) 30 X 20 X 45 = ?
Ans.) 30 X 20 X 45 = ( 30 X 20 ) X 45 = 27000, by associative property
Changing arrangement, 30 X (20 X 45 ) = 27000 , by commutative property
( 30 X 20 ) X 45 = 30 X (20 X 45 ) = 27000.
3) 25 X 20 X 10 = ?
25 X 20 X 10 = ( 25 X 20 ) X 10 = 5000, by associative property
Changing arrangement, 25 X (20 X 10 ) = 5000, by commutative property
( 25 X 20 ) X 10 = 25 X (20 X 10 ) = 5000.
Distributive Property – [ If, a, b & c are whole numbers then a X ( b + c ) = ( a X b ) + ( a X c ) ]
For any whole number a, a X 1 = 1 X a = a
Example –
1) 10 X ( 20 + 15 ) = ( 10 X 20 ) + ( 10 X 15 ) = 200 + 150 = 350
In other way 10 X ( 20 + 15 ) = 10 X 35 = 350
Operation Of Division – [ Dividend = Divisor X Quotient + Remainder ]
As we all know that, if we divide any whole number as a ‘Dividend’ by another whole number as a ‘Divisor’, then the obtained result is considered as ‘Quotient’ and as remaining number would be considered as ‘Remainder’.
DIVISOR ) DIVIDEND ( QUOTIENT
DIVIDEND
------------------- = QUOTIENT
DIVISOR
If there are remainder, then the equation should be
DIVIDEND = DIVISOR X QUOTIENT + REMINDER
DIVISOR ) DIVIDEND ( QUOTIENT
------------------
REMINDER
If there 11 is dividend, 3 is a divisor and 3 is a quotient then remainder would be 2
As per the formula, Dividend = Divisor X Quotient + Remainder
= 3 X 3 + 2 = 11 (Dividend)
Example – 1
1) Divide 175 by 12 and verify the division algorithm
Ans.)
As per the given condition,
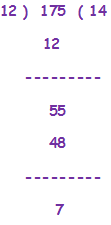
As per the formula,
Dividend = Divisor X Quotient + Remainder
= 12 X 14 + 7 = 168 + 7 = 175
Example – 2
2) Find the largest four-digit number which is exactly divisible by 25.
Ans.) The largest four-digit number is 9999.

Here we can find that, 25 is divisor, 9999 is Dividend, 399 is Quotient, and 24 is remainder.
So as per requirement to find four-digit largest number we have to deduct remainder from 9999,
Hence the required number is
= 9999 – 24 = 9975
Example– 3
Find the smallest five digit number which is exactly divisible by 15.
Ans.) Five digit smallest number is 10000
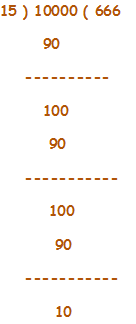
Here we can find that, 15 is the divisor, 10000 is Dividend, 666 is Quotient, and 10 is remainder.
Required number must be greater than 10000, So as per requirement to find five-digit smallest number first I have to deduct remainder 10 from divisor 15 ; 15 – 10 = 5
Thus the required number = 10000 + 5 = 10005
So, the five-digit smallest number is 10005 which is divisible by 15.