CLASS-8
GEOMETRY-ANGLES-PROBLEM & SOLUTION
There are some examples are given below for your better understanding –
Example.1) If an angle is 4/5 of its supplement, find the angles.
Ans.) Let the angle = x⁰, so its supplement = 180⁰ - x⁰
Given that x⁰ = 4/5 (180⁰ - x⁰)
So, 5x⁰ = 4 X 180⁰ - 4x⁰
So, 9x⁰ = 4 X 180⁰
So, x⁰ = 720⁰ / 9 = 80⁰ (Ans.)
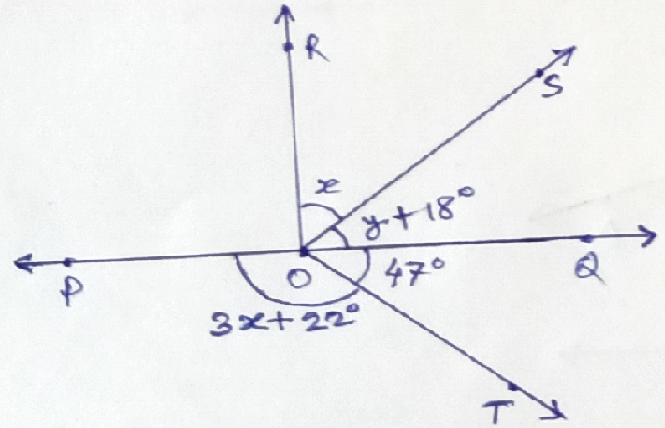
Example.2) Find the values of x& y from the adjoining figure, where POQ is a straight line.
Ans.) here, OT stands on the line PQ. So, ∠POT + ∠QOT = 180⁰,
So, 3x + 22⁰ + 47⁰ = 180⁰
So, 3x = 180⁰ - (22⁰ + 47⁰) = 111⁰
So, x = 111⁰/3 = 37⁰
Being, angles at a point on one side of the line PQ, ∠POR + ∠ROS + ∠SOQ = 180⁰
90⁰ + x + y + 18⁰ = 180⁰
Or, 90⁰ + 37⁰ + y + 18⁰ = 180⁰
Or, y = 180⁰ - 145⁰ = 35⁰
Hence, x = 37⁰ and y = 35⁰ (Ans.)
Example.3) Find the values of x & y from the adjoining figure when x – y = 10⁰
Ans.) ∠COE = vertically opposite ∠DOF = 90⁰
So, sum of the angles at a point on one side of a straight line = 180⁰,
∠AOE + ∠COE + ∠BOC = 180⁰
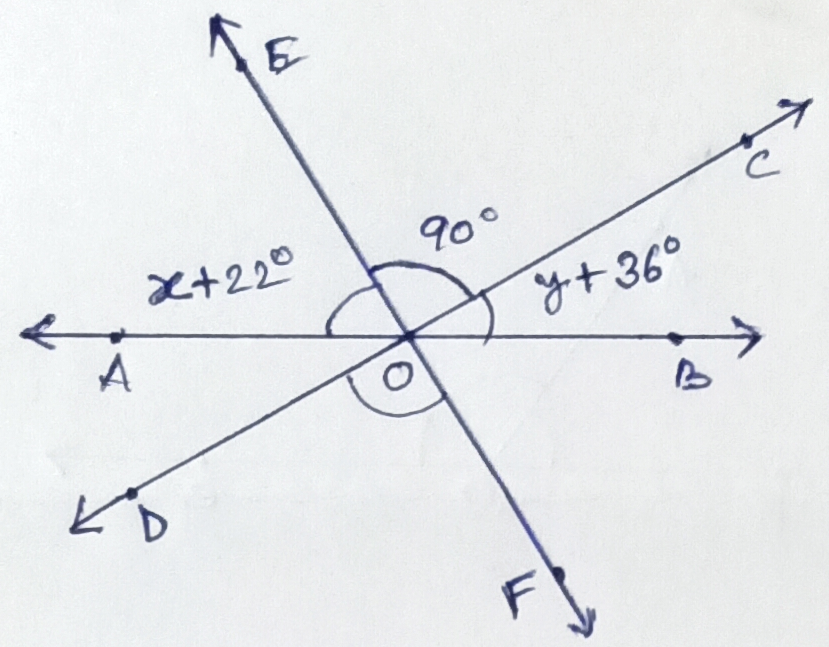
=> x + 22⁰ + 90⁰ + y + 36⁰ = 180⁰
=> x + y + 148⁰ = 180⁰
=> x + y = 32⁰…………………….(1)
And, as per given condition we have, x – y = 10⁰ …………………………..(2)
Now, we will add (1) & (2), and we find -
x + y = 32⁰
x – y = 10⁰
+ - +
----------------------
2x = 42⁰
So, x = 21⁰
Hence, if we put the value of x in equation (1), then we find –
x + y = 32⁰
or, 21⁰ + y = 32⁰
or, y = 32⁰ - 21⁰ = 11⁰
hence, x = 21⁰ & y = 11⁰ (Ans.)
Example.4) Find the value of x, y, & z from the adjoining figure, where x : y : z = 1 : 2 : 3
Ans.) Let, x = a, y = 2a, and z = 3a
Then, 2z + 3y – 3x = 6a + 6a – 3a = 9a,
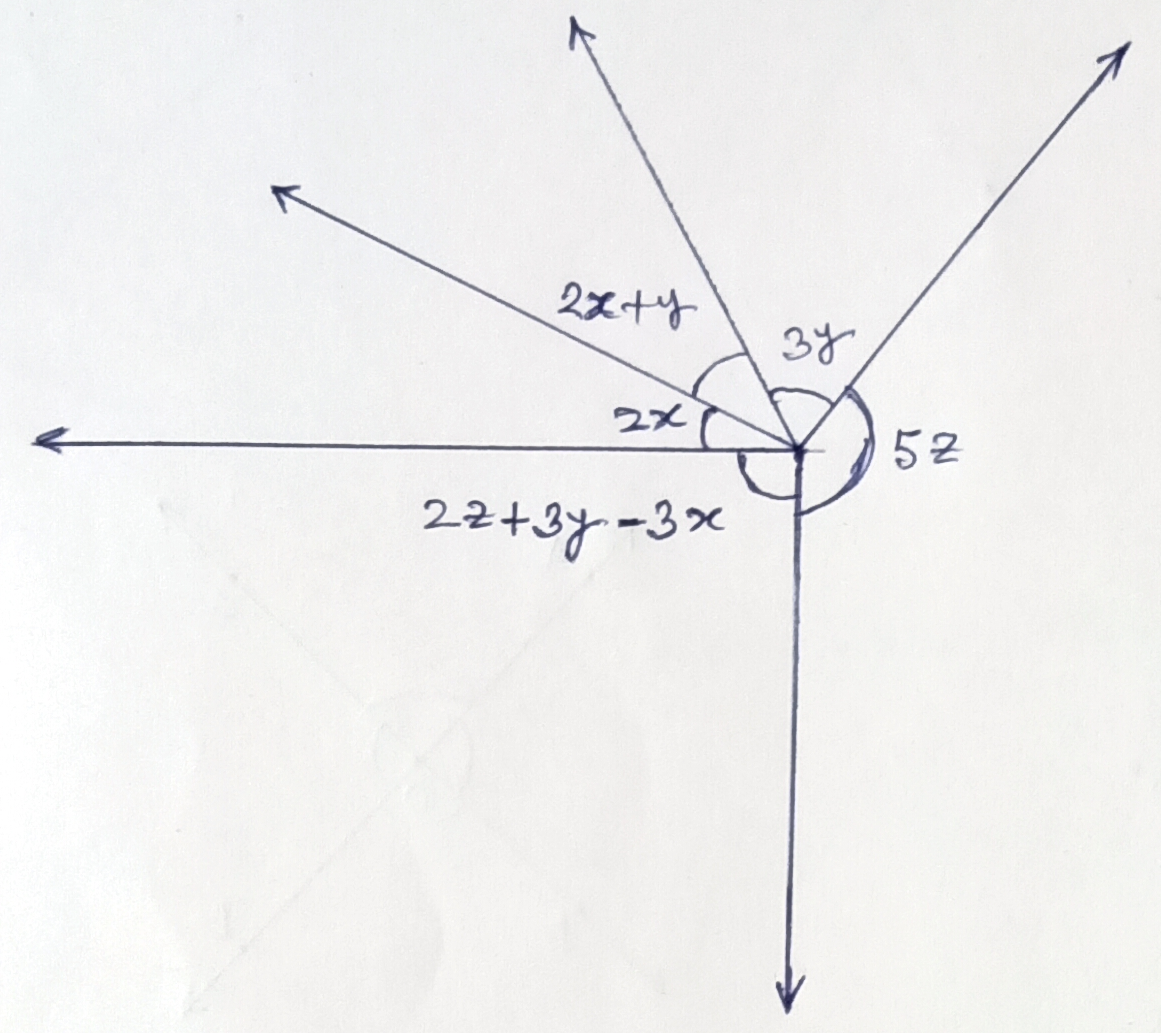
5z = 15a, 3y = 6a
So, 2x + y = 2a + 2a = 4a, and 2x = 2a
So, sum of the angles at a point = 360⁰
So, 9a + 15a + 6a + 4a + 2a = 360⁰
Or, 36a = 360⁰
Or, a = 10⁰ or x = 10⁰
Hence we can find also, y = 20⁰, and z = 30⁰
So, x = 10⁰, y = 20⁰, and z = 30⁰ (Ans.)