CLASS-8
AREA OF RHOMBUS
Area of a Rhombus –
Let, WXYZ is a rhombus, with the diagonals XZ and YW bisecting each other at right angles at the point O
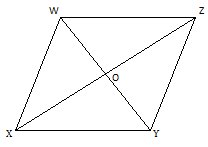
Since WXYZ is also a parallelogram, its area
1
= 2 X area of (∆ WXY) = 2 X ------ (YW) X (OX) =
2
1
= (YW) X (OX) = (YW) X ------ (XZ) [ where OX = 1/2 XZ ]
2
1
= ------- X (YW) X (XZ) = 1/2 X product of its Diagonals
2
1
So, the area of a rhombus = ------- X product of its diagonals
2
Example.) The diagonals of a rhombus are 20 cm & 22 cm. (a) Find its area, (b) the length of a side, and (e) its perimeter.
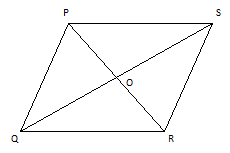
Ans.) Let PQRS is the given rhombus, with its diagonals PR & QS intersecting at the point O
As per the given condition, PR = 20 cm, and QS = 22 cm
1
The area of rhombus = ------ X product of the diagonals
2
1
= ------- X PR X QS
2
1
= ------- X 20 X 22 = 10 X 22 = 220 cm² (Ans.)
2
(b) the diagonals of a rhombus bisects each other at right angles
1 1
OP = ------- PR = ------- X 20 cm = 10 cm
2 2
1 1
OQ = ------- QS = ------- X 22 cm = 11 cm
2 2
And ∆ POQ = 90⁰
In the right angled triangle OPQ, PQ² = OP² + OQ²
So, PQ = √ OP² + OQ² = √10² + 11² = √100 + 121
= √221 = 14.86 = 15 cm (Ans.)
(c) since the sides are equal, so the perimeter of the rhombus = 4 X 15 cm = 60 cm (Ans.)