CLASS-8
CIRCLE - PROBLEM & SOLUTION
Example.1) – In the adjoining figure, find AB and the radius of the circle
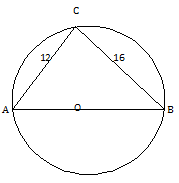
Ans.) An angle in a semicircle = 90⁰ => ∠ACB = 90⁰
In the right angled triangle ABC,
AB² = BC² + CA² = (12² + 16²) cm² = 400 cm²
So, AB = √400 cm² = √20²cm² = 20cm
And, the radius = ½ X AB = ½ X 20cm = 10 cm (Ans.)
Example.2) In the adjoining figure, find OM
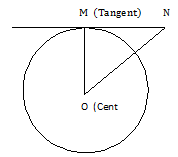
Ans.) MN is a tangent to the circle at M. so, OM ⊥ MN
Now, in the right ∆ OMN,
OM² + MN² = ON²
So, OM = √ON²- MN²
= √17² - 8² cm
= √289 – 64 cm
= √225 = 15 cm (Ans.)
Example.3) In the figure, OA = 6.5 cm and AC = 5cm, Find = BC
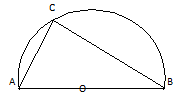
Ans.) An angle in a semicircle = 90⁰ => ∠ACB = 90⁰
AB = 2 X OA
= 2 X 6.5 cm = 13 cm
In the right angles triangle ∆ ABC, AB² = AC² + BC²
=> BC = √ AB² - AC² = √13² - 5²
= √169 – 25 = √144 cm = 12 cm (Ans.)