CLASS-8
SECANT & TANGENT
Secant and Tangent –
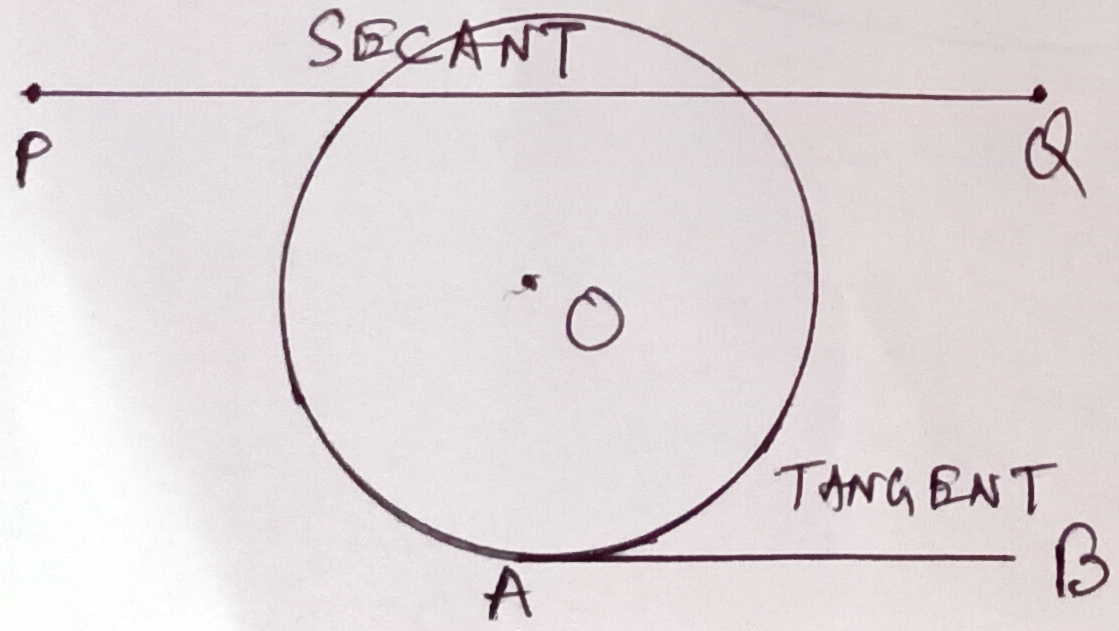
When a straight line that intersects a circle at two distinct points will be considered as a secant of the circle. In the figure, PQ will be considered as a secant of the circle with center at ‘O’.
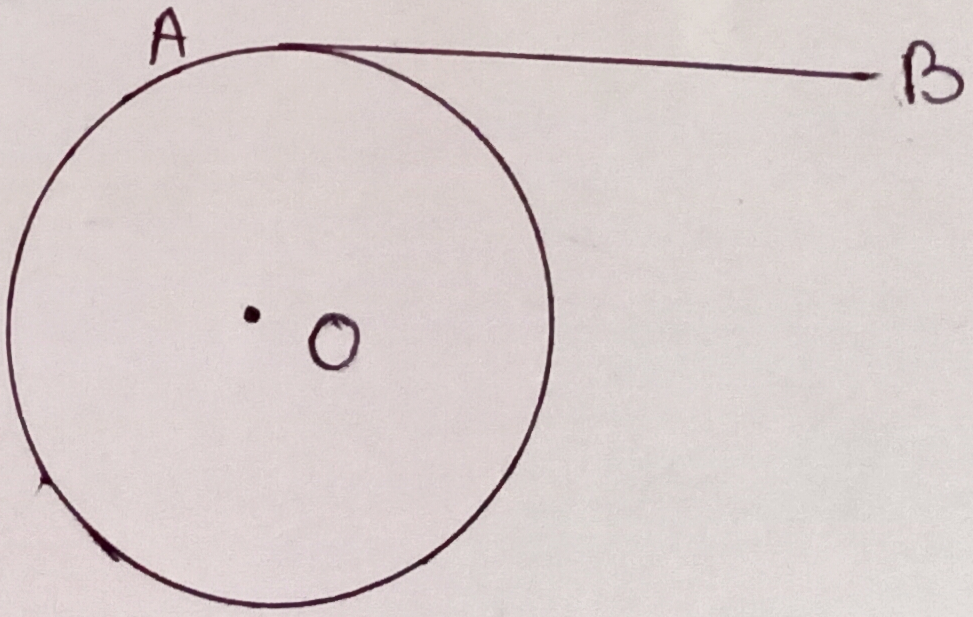
A straight line that intersects a circle at only one point is called a tangent to the circle at that point. In the figure, the line BA is a tangent to the circle at A. The length of the line segment BA is known as the length of the tangent from B and point A is known as the point of contact of the tangent.
Property-1) The Tangent at any point of a circle and the radius through the point should be perpendicular to each other.
In the figure, ∠OAB = 90⁰
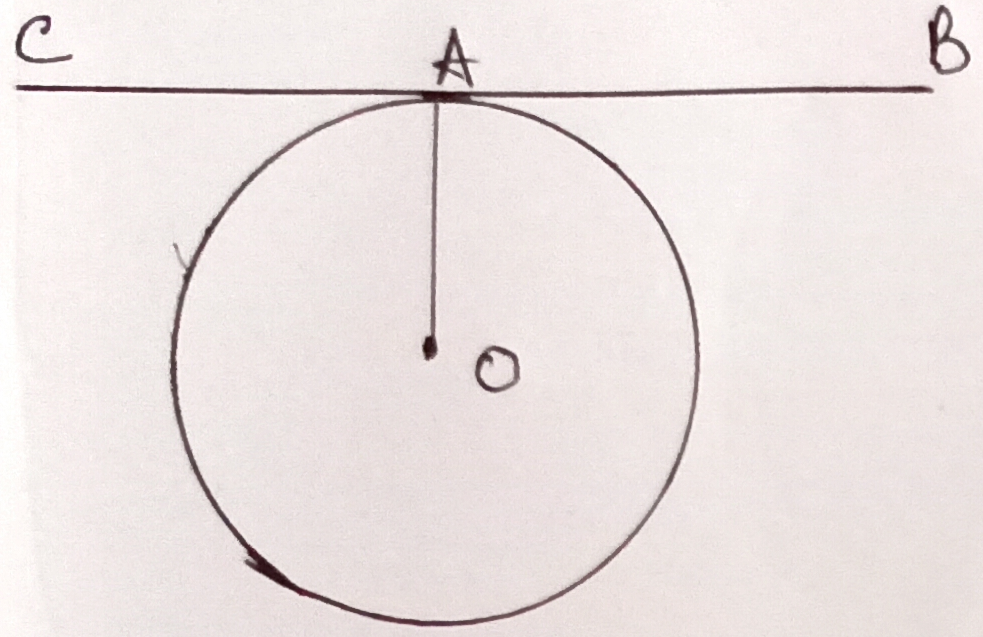
Property-2) There is one, and only one, tangent must be at any point of a circle.
In the figure, since BA and CA are tangents to the circle at A, CAB is a straight line
Property-3) Two tangents can be drawn to a circle from a point that will be situated outside the circle.
In the figure, AD & AE are two tangents to the circle from point A outside the circle.
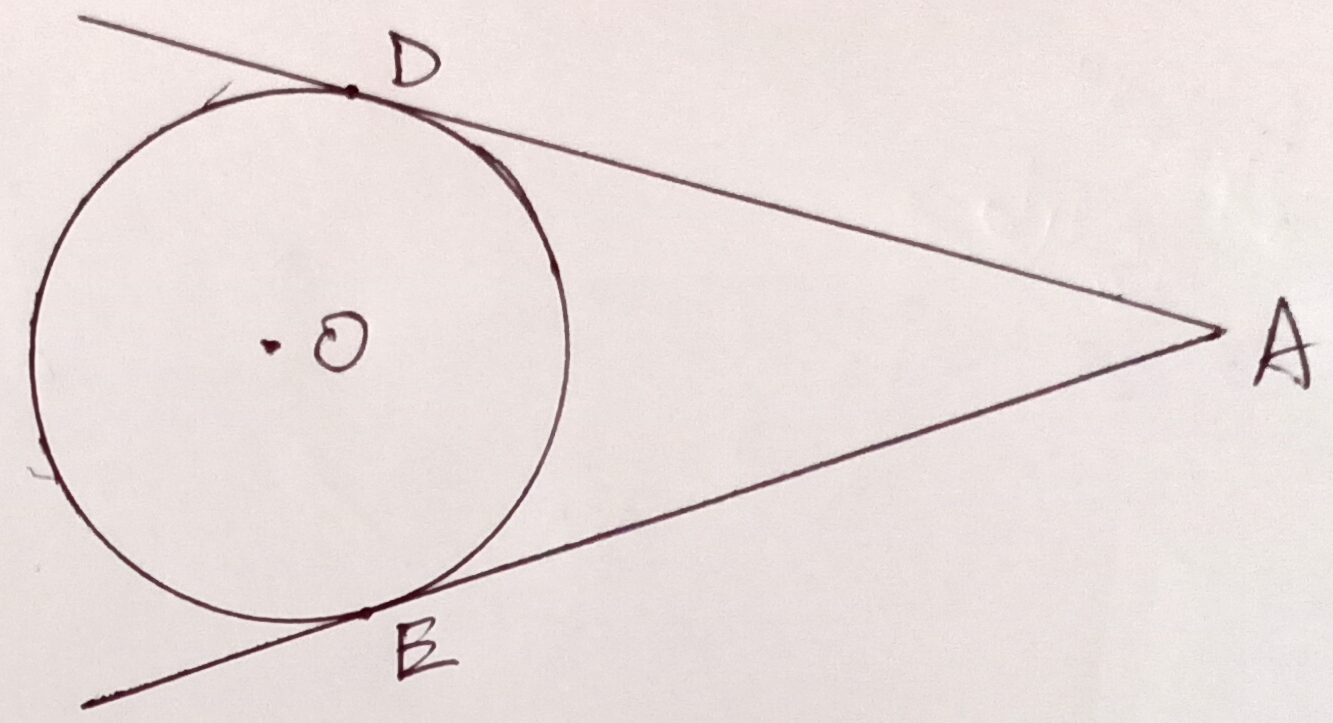
Property-4) If two tangents are drawn to a circle from a point outside the circle then the tangents will be equal in length.
In
the figure, AD & AE are two tangents to the circle drawn from A outside the
circle, so AD = AE